【CSU-2092】解题报告（模拟，物理）

原始题目

2092: Space Golf

  • Time Limit: 1 Sec
  • Memory Limit: 512 Mb
  • Submitted: 77
  • Solved: 35
  • SpecialJudge

Description

You surely have never heard of this new planet surface exploration scheme, as it is being carried out in a project with utmost secrecy. The scheme is expected to cut costs of conventional rover-type mobile explorers considerably, using projected-type equipment nicknamed "observation bullets".

Bullets do not have any active mobile abilities of their own, which is the main reason of their cost-efficiency. Each of the bullets, after being shot out on a launcher given its initial velocity, makes a parabolic trajectory until it touches down. It bounces on the surface and makes another parabolic trajectory. This will be repeated virtually infinitely.

We want each of the bullets to bounce precisely at the respective spot of interest on the planet surface, adjusting its initial velocity. A variety of sensors in the bullet can gather valuable data at this instant of bounce, and send them to the observation base. Although this may sound like a conventional target shooting practice, there are several issues that make the problem more difficult.

  • There may be some obstacles between the launcher and the target spot. The obstacles stand upright and are very thin that we can ignore their widths. Once the bullet touches any of the obstacles, we cannot be sure of its trajectory thereafter. So we have to plan launches to avoid these obstacles.

  • Launching the bullet almost vertically in a speed high enough, we can easily make it hit the target without touching any of the obstacles, but giving a high initial speed is energy-consuming. Energy is extremely precious in space exploration, and the initial speed of the bullet should be minimized. Making the bullet bounce a number of times may make the bullet reach the target with lower initial speed.

  • The bullet should bounce, however, no more than a given number of times. Although the body of the bullet is made strong enough, some of the sensors inside may not stand repetitive shocks. The allowed numbers of bounces vary on the type of the observation bullets.

You are summoned engineering assistance to this project to author a smart program that tells the minimum required initial speed of the bullet to accomplish the mission.

Figure D.1 gives a sketch of a situation, roughly corresponding to the situation of the Sample Input 4 given below.

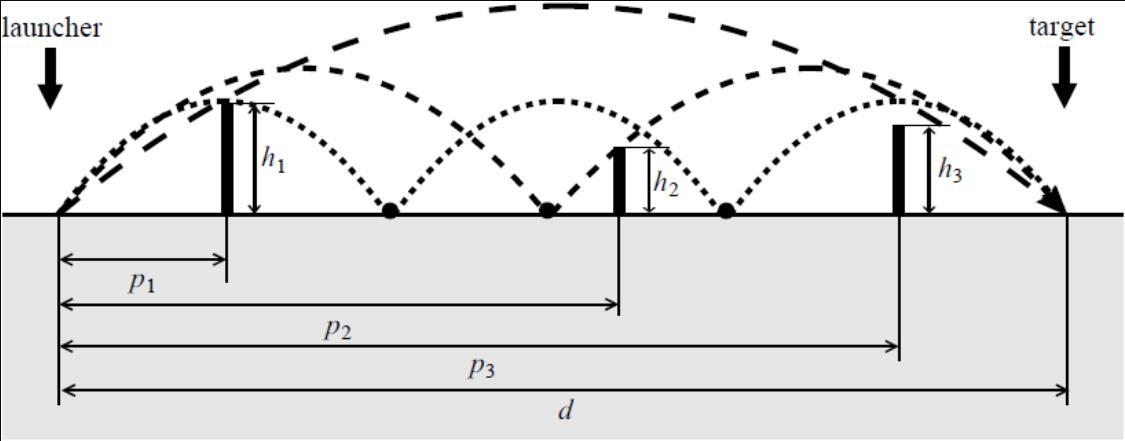
P1.jpg
P1.jpg

Figure D.1. A sample situation

You can assume the following.

  • The atmosphere of the planet is so thin that atmospheric resistance can be ignored.
  • The planet is large enough so that its surface can be approximated to be a completely flat plane.
  • The gravity acceleration can be approximated to be constant up to the highest points a bullet can reach.

These mean that the bullets fly along a perfect parabolic trajectory.

You can also assume the following.

  • The surface of the planet and the bullets are made so hard that bounces can be approximated as elastic collisions. In other words, loss of kinetic energy on bounces can be ignored. As we can also ignore the atmospheric resistance, the velocity of a bullet immediately after a bounce is equal to the velocity immediately after its launch.
  • The bullets are made compact enough to ignore their sizes.
  • The launcher is also built compact enough to ignore its height.

You, a programming genius, may not be an expert in physics. Let us review basics of rigid-body dynamics.

We will describe here the velocity of the bullet \(v\) with its horizontal and vertical components \(v\_x\) and \(v\_y\) (positive meaning upward). The initial velocity has the components \(v\_{ix}\) and \(v\_{iy}\), that is, immediately after the launch of the bullet, \(v\_x = v\_ix\) and \(v\_y = v\_iy\) hold. We denote the horizontal distance of the bullet from the launcher as \(x\) and its altitude as \(y\) at time \(t\).

  • The horizontal velocity component of the bullet is kept constant during its flight when atmospheric resistance is ignored. Thus the horizontal distance from the launcher is proportional to the time elapsed.

\[x=v_{ix}t \tag{1}\]

  • The vertical velocity component vy is gradually decelerated by the gravity. With the gravity acceleration of g, the following differential equation holds during the flight.

\[\frac{d{v_y}}{dt}=-g \tag{2}\]

Solving this with the initial conditions of vy = viy and y = 0 when t = 0, we obtain the following.

\[\begin{eqnarray} y&=&-\frac{1}{2}gt^2+v_{iy}t \tag{3} \\ &=&-(\frac{1}{2}gt-v_{iy})t \tag{4} \end{eqnarray}\]

The equation (4) tells that the bullet reaches the ground again when \(t = \frac{2v\_{iy}}{g}\). Thus, the distance of the point of the bounce from the launcher is \(\frac{2v\_{ix}v\_{iy}}{g}\). In other words, to make the bullet fly the distance of l, the two components of the initial velocity should satisfy \(2v\_{ix}v\_{iy}= lg\).

  • Eliminating the parameter t from the simultaneous equations above, we obtain the following equation that escribes the parabolic trajectory of the bullet.

\[y=-(\frac{g}{2v_{ix}^2})x^2+(\frac{v_{iy}}{v_{ix}})x \tag{5}\]

For ease of computation, a special unit system is used in this project, according to which the gravity acceleration g of the planet is exactly 1.0.

Input

The input consists of several tests case with the following format.

\[d\ n\ b \\ p_1\ h_1 \\ p_2\ h_2 \\ \vdots \\ p_n\ h_n \\\]

For each test, the first line contains three integers, \(d\), \(n\), and \(b\). Here, \(d\) is the distance from the launcher to the target spot \((1 ≤ d ≤ 10000)\), \(n\) is the number of obstacles \((1 ≤ n ≤ 10)\), and \(b\) is the maximum number of bounces allowed, not including the bounce at the target spot \((0 ≤ b ≤ 15)\).

Each of the following \(n\) lines has two integers. In the k-th line, \(pk\) is the position of the k-th obstacle, its distance from the launcher, and hk is its height from the ground level. You can assume that 0 < p1, pk < pk + 1 for \(k = 1,\cdots, n − 1\), and \(pn < d\). You can also assume that \(1 ≤ hk ≤ 10000\) for \(k = 1,\cdots, n\).

Output

Output the smallest possible initial speed vi that makes the bullet reach the target. The initial speed vi of the bullet is defined as follows.

\[v_i=\sqrt{v_{ix}^2+v_{iy}^2}\]

The output should not contain an error greater than 0.0001.

Sample Input

100 1 0
50 100

10 1 0
4 2

100 4 3
20 10
30 10
40 10
50 10

343 3 2
56 42
190 27
286 34

Sample Output

14.57738
3.16228
7.78175
11.08710

Hint

Source

Asia Regional Contest, Tokyo, 2014

题目大意

一道物理题，给定终点和起点的距离\(d\)，以及\(n\)个距离起点坐标不同的障碍物（板子）。 一颗子弹从起点做抛物线运动，可以撞击地面再弹起\(b\)次（忽略能量损失），求可以越过障碍物恰好达到终点的初始速度值大小的最小值。

解题思路

  • 模拟+贪心（不知道可不可以叫贪心）
  • 转化一下，由于撞击地面弹起能量无损失。所以可以将撞击前后的两段转化为一段。对每个可能的距离更新最小值。

\[ d_i=\frac{d}{i} (i=1,2,3 \cdots b-1) \]

  • 对于每个\(d\_i\)，先行判断45度（即\(v\_y=v\_x\)时）是否满足条件，若满足直接更新最小值。若不满足则根据轨迹方程不断更新直至能越过最高点。

解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <cstdio>
#include <cmath>
#include <cstring>
#include <string>
#define INF 0x3f3f3f3f
#define EPS 1e-8

using namespace std;
int n,b;
double d,dis,vx,vy;


//障碍物
struct obstacles{
	double h,x; 
}ob[20];
double x[20]; 

void cal(double x,double h){
	vx=sqrt((dis*x/2.0-x*x/2.0)/h);
	vy=dis/2.0/vx;
}

int judge(){  //判断是否可以跨过所有障碍物 
    for (int i = 0; i < n; i++){
   double h = vy*x[i] / vx - 0.5*x[i]*x[i] / (vx*vx);
   if (ob[i].h-h >= EPS) return 0;
    }
    return 1;
}

double solve(int cnt){
	dis = d/cnt; //划分段
	for(int i=0;i<n;i++) x[i]=fmod(ob[i].x,dis);  //浮点数取模
	vy=vx=sqrt(dis/2); //先检测vy=vx时候
	if(judge()) return vx*sqrt(2.0);
	double ans=INF;
	for(int i=0;i<n;i++){
		cal(x[i],ob[i].h); //根据x[i],ob[i]初的障碍物更新vx vy的值。 
		if(judge()) ans=min(ans,sqrt(vx*vx+vy*vy));
	} 
	return ans; 
	
}


int main(){
	while(~scanf("%lf %d %d", &d, &n, &b))
    {
	memset(ob,0,sizeof(ob));
	memset(x,0,sizeof(x));
    for (int i = 0; i < n; i++) scanf ("%lf %lf", &ob[i].x, &ob[i].h);
    double ans = INF;
    for (int i = 1; i <= b+1; i++) ans = min(ans, solve(i));
    printf ("%.8f\n", ans);
	}
}

收获与反思

  • 从简单开始考虑，无障碍物的时候45度最远
  • 将多段跳跃等效为一段。
  • 浮点数取模函数
    • fmod 函数计算 x 除以 y 的 f 浮点余数，这样 x = i*y + f，其中 i 是整数，f 和 x 有相同的符号，而且 f 的绝对值小于 y 的绝对值。
1
2
3
4
result=fmod(x,y);
printf("10.0%%-3.0= %f/n",result); //1.0
result=fmod(y,x);
printf("-3.0%%10.0= %f/n",result); //-3.0