原始题目

折线分割平面

• Time Limit: 2000/1000 MS (Java/Others)
• Memory Limit: 65536/32768 K (Java/Others)
• Total Submission(s): 37773
• Accepted Submission(s): 25282

Problem Description

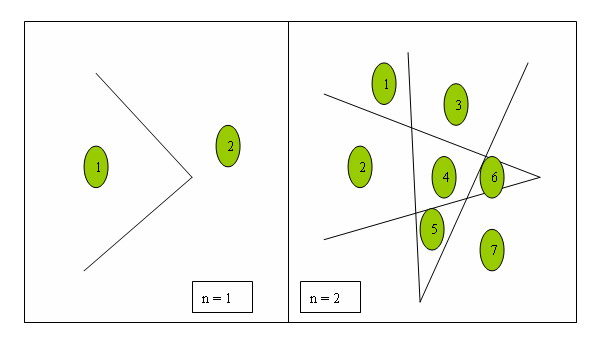
我们看到过很多直线分割平面的题目，今天的这个题目稍微有些变化，我们要求的是n条折线分割平面的最大数目。比如，一条折线可以将平面分成两部分，两条折线最多可以将平面分成7部分，具体如下所示。

1.jpg

Input

输入数据的第一行是一个整数\(C\),表示测试实例的个数，然后是\(C\) 行数据，每行包含一个整数\(n ( 0 < n \le 10000)\),表示折线的数量。

Output

对于每个测试实例，请输出平面的最大分割数，每个实例的输出占一行。

Sample Input

2
1
2

Sample Output

2
7

Author

lcy

Source

递推求解专题练习（For Beginner）

Recommend

lcy

题目大意

如题

解题思路

折线类题目思路：

• dp[i]=dp[i-1]+新增交点数+1

题目数据过大则先手算通项公式。 数据小可以直接递推

解题代码

• 递推写法

#include <cstdio>
#include <cstring>
#include <iostream>
#include <set>
#include <algorithm>
#include <queue>
#include <map>
#include <string>
#define eps 1e-8
#define INF 0x3f3f3f3f
#define rep(i,a,n) for(int i=a;i<n;i++)
#define per(i,a,n) for(int i=n-1;i>=a;i--)
using namespace std;
const int maxn=1e5+5;
typedef long long ll;
ll dp[maxn];
void solve(){
	memset(dp,0,sizeof(dp));
	dp[1]=1;
	dp[2]=2;
	rep(i,3,50){
		dp[i]=dp[i-1]+dp[i-2];
	} 
	
}
using namespace std;
int main(){
	int t;
	solve();
	while(cin>>t){
		rep(i,0,t){
			ll a;
			cin>>a;
			cout<<dp[a]<<endl;
		}
	}
}

• 通项写法

#include <cstdio>
#include <cstring>
#include <iostream>
#include <set>
#include <algorithm>
#include <queue>
#include <map>
#include <string>
#define eps 1e-8
#define INF 0x3f3f3f3f
#define rep(i,a,n) for(int i=a;i<n;i++)
#define per(i,a,n) for(int i=n-1;i>=a;i--)
using namespace std;
const int maxn=1e5+5;
typedef long long ll;


using namespace std;
int main(){
	int t;

	while(cin>>t){
		rep(i,0,t){
			ll a;
			cin>>a;
//			cout<<dp[a]<<endl;
			cout<<(2*a+1)*(a-1)+2<<endl;
		}
	}
}

收获与反思

• Z形线拓展