算法与数据结构学习——线索二叉树

引入

在之前的学习中，我们能够感觉到，二叉树的非递归遍历需要用到栈结构的原因是需要之前遍历的信息。

以二叉链表作为存储结构时，只能找到结点的左、右孩子信息，而不能直接得到结点在任一序列中的前驱和 后继信息，这种信息只能在动态过程中才能得到。

我们想保存这个信息，该怎么办？

通过考察各种二叉链表，不管形态如何，空链域的个数总是多过非空链域的个数。 准确的说，n 个结点的二叉链表共有 2n 个链域，非空链域为 n-1 个，其中的空链域必定有 n+1 个。如下图所示。

1.png
1.png

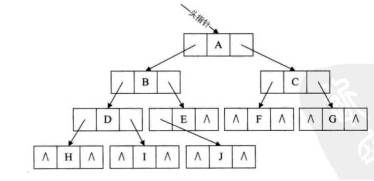
实际上，我们可以利用好这些空链域来存放结点的前驱和后继信息。

线索二叉树

1
2
3
4
5
6
7
8
9
10
11
// 二叉树的二叉线索存储表示
typedef enum PointerTag
{
    Link,
    Thread
}; //0 为孩子指针  1为线索指针
typedef struct BiThrNode
{
    TElemType data;
    struct BiThrNode *lchild, *rchild; //左右孩子/线索指针
    PointerTag LTag, RTag;             //左右标识

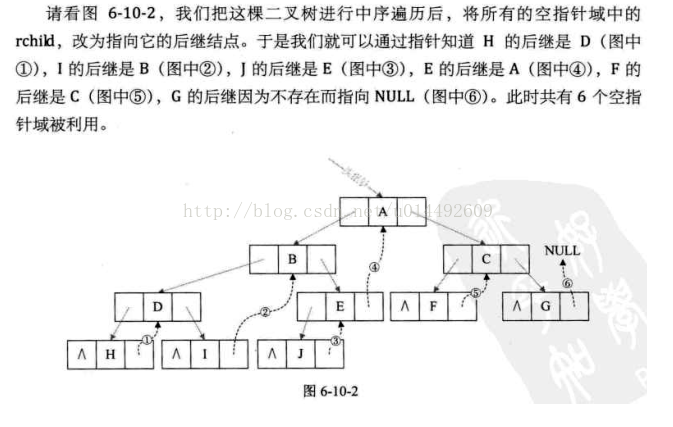
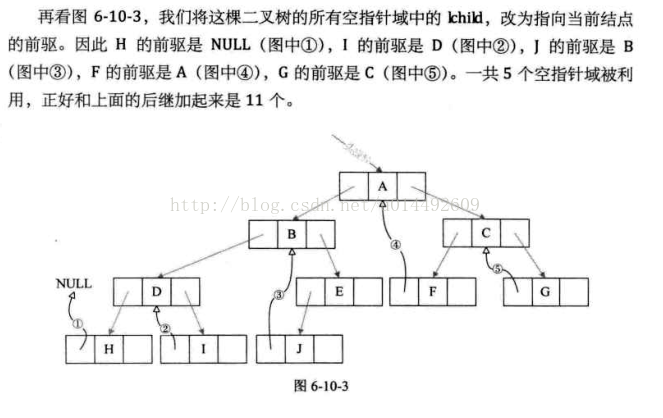
线索化的实质就是将二叉链表中的空指针改为指向前驱或后继的线索。 由于前驱和后继信息只有在遍历该二叉树时才能得到， 所以，线索化的过程就是在遍历的过程中修改空指针的过程。 遍历即线索化过程。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
BiThrTree pre; //表示遍历的上一点
void InThreading(BiThrTree p)
{
    if (p)
    {
        InThreading(p->lchild); //遍历左子树
        if (!p->lchild)         //当前点没有左孩子
        {
            p->LTag = Thread; //前驱线索标记
            p->lchild = pre;  //左孩子指针指向前驱
        }
        if (!pre->rchild) //前驱点没有右孩子
        {
            pre->RTag = Thread; //后继线索标记
            pre->rchild = p;    //右孩子指针指向后继
        }
        pre = p;
        InThreading(p->rchild); //遍历右子树
    }
}

中间代码做的事情：

对中间结点的左孩子判断（是否存在直接前驱），如果不存在的话左孩子的指针并不是空，而是指向保存的前驱结点。 同时对前驱结点的右孩子判断（是否存在直接后继），如果不存在的话指向当前的结点。

如图：

2.png
2.png
3.png
3.png

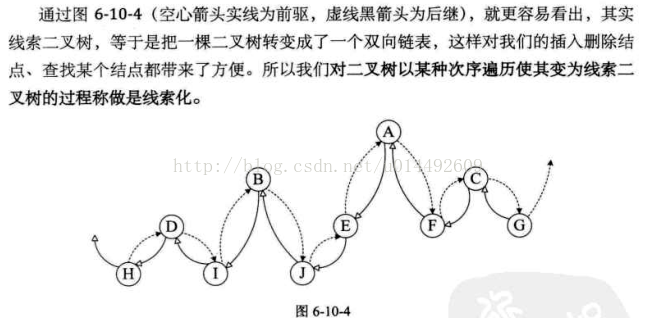
完成前驱和后继以后，线索二叉树的遍历，实际上等于操作一个双向链表结构。

如图：

4.png
4.png

参考博客

彻底理解线索二叉树