本文主要内容主要来自Chaum van Antwerpen在89年发表的《Undeniable Signatures》一文以及Gennaro、Krawczyk和Rabin在97年发表的《RSA-Based Undeniable Signatures》一文，用来了解不可否认签名方案的相关知识。

介绍

背景介绍

数字签名的复制属性不同于我们现实生活中的签名文件，在不考虑时间戳的前提下，我们基本上可以认为复制签名和原始签名是相同的。这种极易复制的性质在很多场合下是有利的，比如带签名公告的分发，开源软件的认证，这种性质多要求带签名的副本对分发无抵抗要求（甚至是希望分发）。

但它不适合许多其他应用程序。对于在某种程度上对个人或商业敏感的所有书面或口头承诺的电子替代品。 在这种情况下，经核证的副本的扩散可能会导致勒索，或者工业间谍的非法利用。这种承诺的接受者当然应该能够确保发行人以后不能否认它，但未经发行人同意，接收方也不能向其他任何人展示承诺。

不可否认的签名非常适合这种应用程序。不可否认签名(如数字签名)是由签名者发出的数字，它取决于签名者的公钥和签名的消息。然而，与数字签名不同的是，不可否认的签名如果没有签名者的合作是无法验证的。

不可否认签名

不可否认签名概念由Chaum和van Antwerpen在[1]（89年）首先提出。它拓展了普通签名的概念，使用强不可否认性，且对签名的验证要求在签署者（证明者）的参与下完成。这以性质有效的防止了带签名的有价值文件的多次拷贝分发的滥用情况，在一些特殊场合下起到了作用。下面具体说明不可否认性质的含义以及不可否认签名的应用。

不可否认性质

不可否认性质包括两层含义：

1. 签名的证实和否定必须与签名者合作完成，这一点可以有效地防止一些有价值文件被随意的复制或分发；
2. 签名者不能抵赖它曾签过的签名，由于他曾签过的签名可以通过拒绝执行证实协议来否认他曾签过的签名，为了防止此类事件发生，不可否认签名增加了一个否认协议，签名者可以利用否认协议证明一个伪造的签名是假的；而如果签名者拒绝执行否认协议，就表明签名事实上是由他签署的。

论文中提出基于RSA的第一个不可否认的签名方案。 自1989年引入以来，大量工作一直致力于研究不可否认的签名。 到目前为止，这项工作一直基于离散对数系统。 相反，我们的方案使用常规RSA签名来生成不可否认的签名。 在这个新设置中，RSA的签名和验证指数都由签名者保密，而公钥由单个公共消息上的复合模数和样本RSA签名组成。

我们的方案具有一些吸引人的特性：首先是可证明的安全性，伪造不可否认的签名与伪造常规RSA签名一样困难。其次，确认和拒绝协议都是零知识（特别是，确认协议仅涉及两轮通信和少量取幂）。此外，我们的方案的基于RSA的结构提供了简单而优雅的解决方案，以提供最初引入不可否认签名的文献中发现的不可否认签名的几个更高级的属性，包括不可否认签名的可转换性（转换为可公开验证的签名），委托确认能力的可能性，拒绝签名给第三方而不放弃签署的权力，以及签名和确认操作的分布式（阈值）版本的存在。

由于上述属性以及我们的不可否认的签名与标准RSA签名相同的事实，我们提出的方案对于实际实现来说，它变得非常有吸引力。

预备知识

1

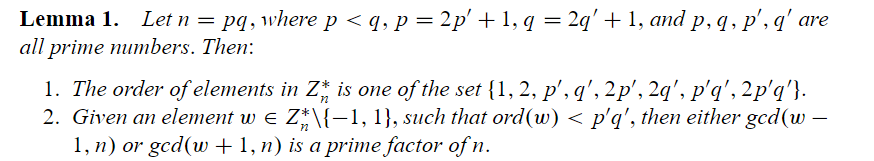
引理 1：

令 \(n=pq\)，且\(p<q\)，\(p=2p'+1\)，\(q=2q'+1\)，\(p\)，\(q\)，\(p'\)，\(q'\)均为质数，则：

1. \(Z_n^{*}\)中的任意元素的阶均在集合\(\{1,2,p',q',2p',2q',p'q',2p'q'\}\)中。
2. 对于给定的\(w\)满足\(w \in Z_n^{*} \setminus \{ -1 , 1 \}\)，且\(ord(w)<p'q'\)，则\(gcd(w-1,n)\)或\(gcd(w+1,n)\)是n的一个素因子。

2

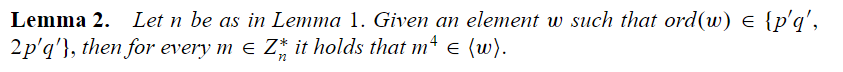
引理 2：

令\(n\)同引理1中规定，对于给定的\(w\)满足\(ord(w) \in \{ p'q', 2p'q' \}\)，则对于任意\(m \in Z_n^{*}\) , \(m^4 \in \langle w \rangle\)

新的不可否认签名方案

在这一节，我们给出我们方案的细节，首先我们定义如下集合。 \[N= \{ n | n = pq, p<q , p = 2 p'+1, q= 2q'+1\}\]

其中\(p\)，\(q\)，\(p'\)，\(q'\)均为质数。该系统由签名者根据通过以下方式设置。从该集合里随机选取一个元素\(n\)，选择\(e,d \in [ \varphi(n) ]\), 满足\(ed \equiv 1 \mod { \varphi (n) }\)；选择一对\((w,S_w)\)满足\(w \in Z_n^{*}, w \not ={1} , S_w = w^{d} \mod {n}\)，公钥参数为\((n,w,S_w)\)，私钥参数为\((e,d)\),

我们用\(PK\)表示所有按照上述方法生成的\((n,w,S_w)\)元组。关于公钥形式的选择以及如何验证其正确性，请参见4.3节。特别地，这里体现出，\(w\)可以被设置为一个固定的值。比如总是设置为\(w = 2\)，这种简化提高了公钥系统计算以\(w\)为基数的幂的效率。

生成一个签名

为了在消息上生成签名，签名者执行常规RSA签名操作，即，他计算\(S_m = m^{d} \mod {n}\)，得到输出\((m, S_m)\)，更准确地说，在应用求幂之前首先通过合适的编码（比如通过单向哈希函数）处理消息，使得生成的签名方案面对选择明文攻击依旧可以假定是不可伪造的（需要说明，普通RSA没有这个属性）。给定一个消息\(m\)，我们认为\(\overset{\rm -}{m}\)为编码输出后的消息，因此，\(S_{\overset{\rm -}{m} } \overset{\rm def}{=} {\overset{\rm -}{m}}^{d}\)，我们稍稍泛用了\(S_w\)来表示\(w^{d} \mod {n}\)，且用\(w\)而非\(\overset{\rm -}{w}\)。

确认协议

我们提出了一个确认签名的协议。 它由两个玩家，证明者和验证者执行。 协议的公共输入是公钥参数，即\((n,w,S_w) \in PK\)，以及\((m,S_m)\)。如果\(S_m\)是有效签名，则\(P\)将可以说服\(V\)这个事实，反之如果不是有效的，则除了一个微不足道的概率，没有任何证明者（即使是一个计算上无界的证明者）能够让\(V\)相信这个签名是有效的。

3

协议的想法是产生一个相关的元素，该元素对签名者来说是随机的，并且验证者签名（假设消息\(m\)上的签名是正确的）。 这个“盲”元素是通过消息\(m\)取\(i\)次幂来创建的，以及他的（正确的签名是公知的）。 直观地说，作弊证明者需要找到作为骗子的价值。 然而，有许多指数给出了相同的结果，并且我们证明了证明者（即使计算上无界）也无法区分它们。

该协议的一个有趣的方面是证明者可以成功说服验证者接受签名，多一个参数的签名多个签名，在设计拒绝协议时，我们确保签名者不能拒绝此扩展形式的签名，\(SIG(m) \overset{\rm def}{=} \alpha \overset{\rm -}{m}^{d}, ord(\alpha) ≤ 2\).

为了便于说明，确认协议出现了零知识协议版本，有一些众所周知的技术[GMW]，[BCC]，[Go]使用概念函数的概念将零知识属性添加到上述协议：

在第2步中，\(P\)，不再发送\(A\)而是发送一个承诺\(commit(A)\)，当\(V\)向\(P\)揭示\(i,j\)的值时，在检查\(Q \overset{\rm def}{ = } {S_m^{2i}}{S_w^{j}} \mod n\)，\(P\)再将\(A\)告诉\(V\)，则验证者检查\(A\)是否符合之前的承诺，然后进行上述协议的第三步。

通过承诺函数的性质实现零知识条件，即

1. \(commit(x)\)不反应关于\(x\)的任何信息（对破译有用处的任何信息）
2. \(P\)不能找到\(x'\)使得\(commit(x) = commit(x')\)

承诺函数可以通过多种方式实现，比如简单的用语义安全的RSA加密\(A\)，而验证者不知道私钥，如果想打开这个承诺，应用概率加密，这是一个有效的方法，因为不存在长幂运算。

定理 1（确认定理）

证明对于任意符合定义要求的\((n,w,S_w) \in PK\)，确认协议均具备完整性，健壮性和零知识。

完整性：偶次幂消除了二阶的因子\(\alpha\)的影响，我们允许这样的签名。

健壮性：我们试图说明，当签名无效时\(P\)说服\(V\)接受签名的概率由选择\(A\)通过\(V\)的测试的最大概率决定。我们可以证明（证明过程见原文章）概率为\({\pi}_1+{\pi}_2 < \frac{\varphi(n)}{ord(\alpha) ord(w)} + \frac{2(n - \varphi (n))}{n}\)，结合引理1我们又易得到\(ord(w) ≥ p'q'\)，欺骗者不知道关于\(n\)的因式分解信息，以及\(ord(\alpha) ≥ p'\)，所以我们能得到\({\pi}_2 < \frac{4}{p'}\)，以及\({\pi}_1 + {\pi}_2 < \frac{6}{p'}\)由于\(p'\)也是一个相当大的质数，所以实际概率很小。

零知识：见前述协议详情。

拒绝协议

图2展示了拒绝协议。 协议的公共输入是公钥参数，即\((n,w,S_w) \in PK\)，以及\((m,S_m)\)。如果\(S_m\)不是有效签名，那么\(P\)能够说服\(V\)这个事实，若签名效，\(P\)能够说服\(V\)该签名无效的概率可以忽略不计。

我们的解决方案是基于 由Chaum [Ch1]引入的协议，旨在用零知识的一个素数域上两个元素的离散对数的不等式。 上述论文中提到的协议和证明对于对\(n\)为合数的简化剩余系不具备有效性，特别地，是因为它们依赖一个简化剩余系地生成器（而我们已经证明符合我们要求地简化剩余系的最大阶并不等于群的阶）。 不过，一个针对上述协议的细致改良版本以及一个相关的证明方法会被用来证明解决在\(n\)为合数的简化剩余系问题。

4

该协议以下面的方式工作，验证者在第一步中给出两个证明者可以使用验证指数\(e\)验证的两个值（通过商值\({( \frac{ \overset{\rm -}{m} }{S_m^e} })^{i}\)来验证 ）。仅当正民者可以找到选定\(i\)值时，验证者才接受协议的运行。如果\(S_m\)不是消息\(m\)的有效签名，则\(P\)，需要彻底搜索\(i\)应取值的范围，然而，如果\(S_m\)时有效签名，无论\(i\)的取值为多少，上述商式的结果恒等于\(1\)，那么证明者不能获取到关于\(i\)的任何信息从而只能猜测\(i\)的值（来达到欺骗的目的）。

为了实现对\(i\)的穷尽搜索，一个人需要选择一个尽可能小的范围，如果上界设置为某个值\(k\)，则证明着需要对\(\frac{ \overset{\rm -}{m} }{S_m^e}\)进行\(k\)次乘法操作来找到\(i\)。因而该协议具有\(\frac{1}{k}\)的出错概率。因为注意到选择\(k\)的时间复杂度为\(O( \log n )\)，那么穷举搜索的成本大概相当于单个的长幂运算。另一方面，这种情况下欺骗的概率为\(\frac{1}{k}\)。我们以\(k = 1024\)为例，我们可以重复该协议十次，则可以实现\(\frac{1}{2^{100}}\)的安全性。正如在引言中所述，相对于运行欺骗概率为\(\frac{1}{2}\)的子协议，效率要高十倍。

下图展示了协议流程（忽略了零知识的步骤），这与确认协议的情况类似。然而，在这个协议中，需要在第2步中特殊对待。如果一个（诚实）的证明者并没有找到一个满足等式的\(i\)值，那么就意味着\(V\)是在欺骗，\(P\)中止协议的执行。虽然终止协议中没有泄露很多信息，但它确实揭示了一部分，在零知识版主中我们甚至连这些信息都不想泄露。因而，\(P\)应当继续协议的执行并在“假承诺”中提交0值。这样会掩盖\(i\)值被发现与否的信息。需要指明在\(i\)值没有被找到的情况下，验证者会被曝光为欺骗者从而0的承诺将不会被揭示。

定理 2（拒绝定理）

证明对于任意符合定义要求的\((n,w,S_w) \in PK\)，确认协议均具备完整性，健壮性和零知识。

完整性：即对于\(S_m \notin SIG(m)\)，若两人均遵守协议的执行，那么\(V\)总会接受\(S_m\)不是消息\(m\)的一个合法签名。

健壮性：即对于\(S_m \in SIG(m)\)，那么一个骗子证明者\(P^{*}\)即便计算能力无上界，无法以大于\(\frac{1}{k}+ \frac{O(1)}{p'}\)的概率说服\(V\)拒绝该签名（不认为该签名合法）。

零知识：该协议是零知识的，对于输入的消息和不合法签名，任何（很可能是骗子）验证者\(V^{*}\)与证明者\(P\)的交互中都不会获取除了\(S_m\)是个非法签名外的任何信息。

验证过程需要再学习。

安全性分析

文章这里不对不可否认签名的安全性要求做正式分析，关于这种正确且完整的处理，我们建议读者参考Damgard和Pedersen的论文[DP]；这些概念的概述可以在我们的介绍中找到（特别是在1.1节）。这里我们基于该大纲以及前一节中零知识证明结果来讨论我们解决方案的安全性。

签名的不可伪造性

我们证明如下定理

定理 3

假定基础RSA签名是不可伪造的（对已知明文或者选择明文攻击），则我们的不可否认签名方案对相同攻击也是不可伪造的。

如前所述，RSA不能直接抵抗选择明文攻击，但我们通过其他方法来解决这个问题，例如，在取幂之前对消息进行适当的编码（参见3.1节）。

假设存在一个伪造者\(F\)，在接收到不可否认的公钥对，并与签名者进行确认和拒绝协议交互后，它可以在我们的方案中伪造不可否认的签名。即可以输出\((m,S_m)\)且\(S_m \in SIG(m)\)。我们构建了一个攻击者\(A\)，他将使用此伪造和伪造的常规RSA签名。给定RSA公钥\((n,e)\)，若\(A\)想要伪造一个签名他需要按照如下步骤操作，首先选择一个随机值，并将不可否认签名的模式的公钥对设置为\((n,w=r^e \mod n, S_w = r)\)并且将这些值交给\(F\),当\(F\)请求一个在\(m\)上的不可否认签名时，攻击者\(A\)请求\(S\)取签署消息并且将其交给\(F\)这个签名对\(m,S_m\)，当\(F\)请求对\(F\)提供的对\(m,S\)验证时，\(A\)首先检查\(S_m\)是否等于\(S\)，从而与\(F\)执行确认或拒绝协议（仅需知道\(e\)即可）。经过这一步骤后，伪造者\(F\)就可以产生一个伪造的我们设计的不可否认签名方案。

签名的不可分辨性

不可否认签名的基本目标是，没有人能够在不与合法签名者进行协议交互的情况下验证消息及其(声称的)签名的有效性。根据[DP]指出，我们需要证明公钥信息和任何消息\(m\)（但不是签名指数\(d\)），一个人可以模拟出\(m\)的签名，从分布的意义上说，模拟签名不能和有效签名区分开。我们通过以下方式实现该属性，给定任何消息，我们对其底层RSA确定的编码，然后将消息随机幂次模\(n\)，那么与真实签名的差别即下面等式。

\[\log {(s(m))} \overset{\rm ?}{=} \log {(S_w)}\]

\(Z_n^*\)上的离散对数难题，这个问题还没有有效解法，尽管它与RSA，因子分解或者离散对数问题的等价性尚未建立，因此我们需要以下难以处理的假设，以用来描述模拟前面和真实签名的硬度差别。

假设EDL

对于值\(n,w,S_w, \overset{\rm -}{m},s(w)\)，他们对于离散对数的等式是不可分辨的。

我们的假设建立\(e,d\)保密，因为我们的方案公钥中并不含\(e\)，并且协议是零知识的。

注意，对消息编码是我们假设的一部分，我们强调，模素数的模拟假设对于声称先前不可变签名方案的安全性也是必要的（参见[DP]）。 然而，虽然我们可以证明EDL假设意味着我们签名的可模拟性，但在[DP]中这个含义并未得到证实，但只是推测为。

定理 4

根据上述EDL假设，我们的签名是可模拟的，因此如果没有签名者或其委托的确认者/合作就无法验证。

选择签名者的密钥

在第3节中，我们定义了签名者的公共和私有参数应该是什么。 我们对确认和拒绝协议的（强壮性）分析取决于正确选择的这些参数。 通常，只要签名者向可信方（例如，认证机构）注册该公钥，就可以进行该公钥的验证。 在这里，我们概述了用于检查模数\(n\)的正确组成，\(w\)以及\(S_w\)是\(w\)的幂，的协议。（作为签名者对签名的“承诺”）。 请注意，这些协议仅在注册时间执行一次。 我们用作为这些参数的验证者的实体表示，并通过证明其正确选择的签名者。这些协议仅在注册时间执行一次。这里我们用\(V\)表示验证参数有效性的实体，\(P\)表示希望证明参数有效性的证明者。

验证\(w\)是高阶的

根据引理1，如果\(w \notin \{-1,1 \}\)，并且\(gcd(w-1,n)\)并不是\(n\)的因子。事实上，我们可以选择固定的\(w\)值，比如\(w=2\)，对于所有不可否认签名，这个选值总能顺利通过验证（或者因子是可分解的。）

验证\(S_w \in \langle w \rangle\)

下面的协议基本上是证明[CEG]中证明的离散对数协议，再一次修改了模数以便能够使用合数模量。签署者\(P\)选择一个值\(r \in _r [ \varphi (n)]\)，并且将其交给\(V\)值\(w' = w^r\)。验证者\(V\)用以随机位\(b\)回复（不经意传输）。如果\(b=0\)，则\(P\)返回值\(r\)，若\(b=1\)，则\(P\)返回值\(d+r \mod \varphi(n)\)。在第一种情况下，\(V\)检查是否\(w^r = w'\)，而在第二种情况下，检查是否\(w^{d+r} = w' S_w\)，若\(w \notin \langle w \rangle\)，那么\(P\)通过测试的概率为\(\frac{1}{2}\)，重复这个测试\(k\)次，那么欺骗概率降低到\(\frac{1}{2^k}\)。（有些像不透露\(d\)的零知识证明，d，e都在私钥对中）。事实上，如果我们假设存在一个理想的哈希函数，那么协议可以非交互的执行。

拓展

该协议适用相关文献中提到的关于不可否认签名的性质的拓展。

可转换的不可否认签名

这种最早出现在[BCDP]中，并最早在[DP]中提出了基于ElGamal签名的安全方案。可转换的不可否认签名允许签名者可以通过发布一个（或者多个值）将不可否认签名转换为常规（即可以不同过与签名者交互自身验证）数字签名。在我们的方案中，只要公布\(e\)的值就可以轻松转化为传统的RSA签名。转化方案的安全性（即不可伪造性）暗示了该转化方案的安全性。

授权委派

这个想法是希望能让签名者向第三方授权确认或否认能力，但不向其提供签名的能力。 在很多文献中，这一概念通常在签名的可转换性上下文中解释。但是，这两个概念是不同的。

显然，如果公开的话，那会将该不可否认签名转化为可普遍验证的签名。然而，然而，反过来却未必正确。转换签名的信息如果秘密交给第三方，可能依旧不允许该方以不可转让的方式证明签名的真伪。在我们的设置中，签名者可以简单地给第三方密钥，这是唯一需要的信息，用来成功地执行拒绝和确认协议。且显然，\(e\)的接受方并不能自己签署文件，这基于常规RSA签名的性质。

分布式证明者（签署者）