【CSU-2187】解题报告（维护顺序极差）

原始题目

2187: 翻转游戏加强版

  • Time Limit: 1 Sec
  • Memory Limit: 128 Mb
  • Submitted: 101
  • Solved: 23

Description

给当一个01串，最多可以对一段区间里的01取反一次，求最多能取得的1的个数

Input

多组数据，第一行为数组组数\(T(T≤10)\)

每组数据第一行一个整数\(N(1≤N≤{10}^{6})\)

第二行一个长度为\(N\)的01字符串

Output

每组数据输出一行代表答案

Sample Input

2
4
1001
4
1111

Sample Output

4
4

Hint

Source

题目大意

如题

解题思路

  • 小规模数据采取枚举分界点的方法，时间复杂度\(O(n^{2})\)

  • 仔细想一下，我们要找的是一个区间，里面0的数量与1的数量差最大。如果直接寻找区间有点难理解的话，我们 可以换一个角度，记录出现0和出现1的差值，求差值在翻转以后的最小值。

如图

1.png
1.png

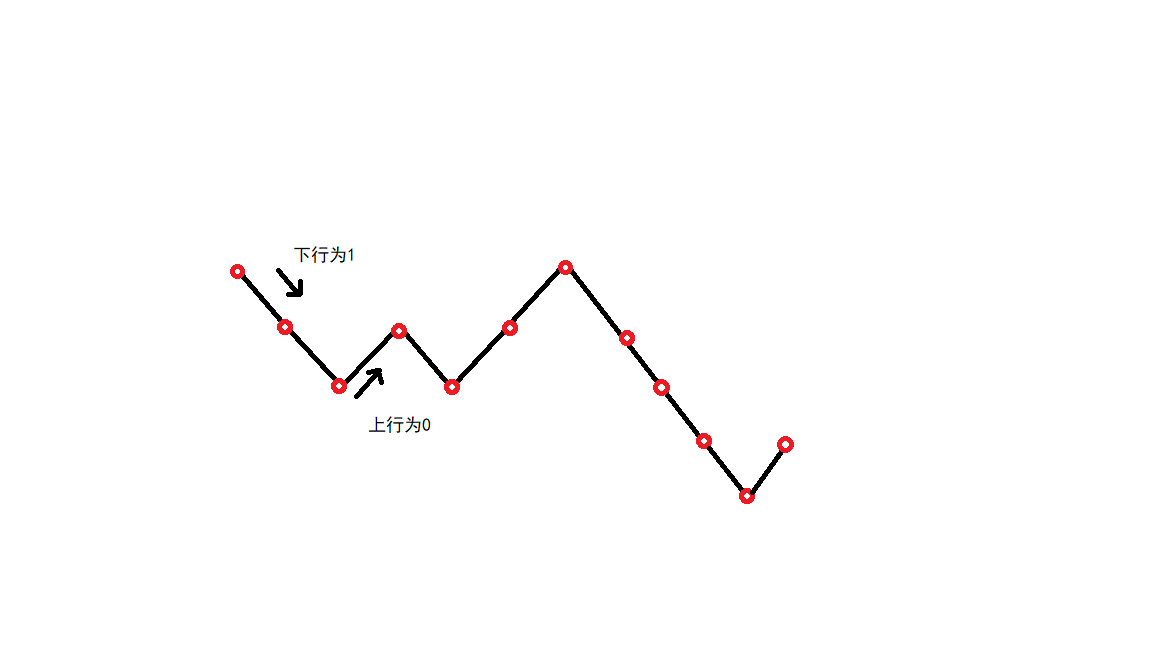
  • 那么如何求翻转以后的最小值？如果对每个区间下限进行计数，遇1减减，遇0加加，我们的答案就是不同起点的所有cnt值得最大值。

  • 实际上我们就是找图中一个极小值（包括头点）与一个极大值（包括末尾）极差得最大值，而且需要注意得是我们求的是1的翻转次数最大，所以要求是一个极小值在左，极大值在右，左低右高。

再如图

2.png
2.png
3.png
3.png
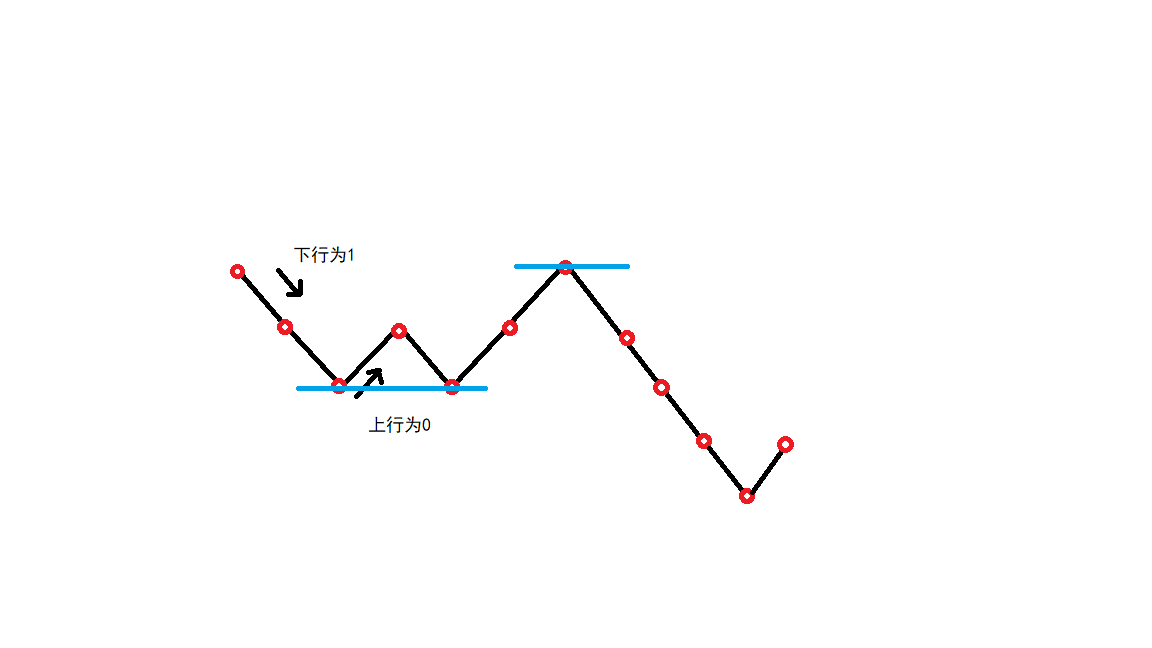
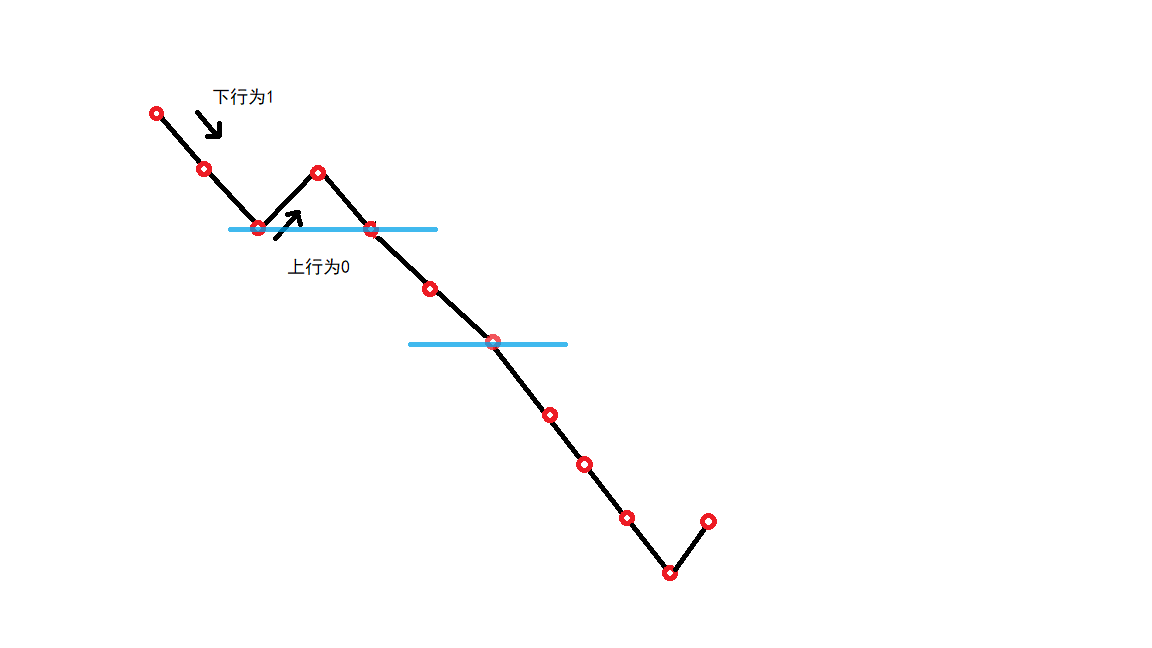
  • 线性从头扫一遍，维护最小值，同时重新计数cnt，最后求cnt的最大值。

解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include <cstdio>
#include <cstring>
#include <queue>
#include <stack>
#include <cstring>
#include <algorithm>
#include <vector>
#include <string>
#include <bits/stdc++.h>
using namespace std;
const int maxn=1e6+5;
const int maxm=1e6+5;


#define INF 0x3f3f3f3f
#define EPS 1e-8
#define rep(i,a,n) for(int i=a;i<n;++i)
#define per(i,a,n) for(int i=n-1;i>=a;--i)
#define fi first
#define se second
#define pb push_back
#define np next_permutation
#define mp make_pair

typedef long long ll;
typedef unsigned long long ull;
typedef vector <int> vi;
typedef pair<string,string> pss;

typedef pair<int, int> pii;

int main(){
    ios::sync_with_stdio(false);
//    freopen("in.txt","r",stdin);
    int t;
    cin>>t;
    while(t--){
   int n;
   cin>>n;
   string s;
   cin>>s;
   int ans=0,cnt=0,ccnt=0;
   int mmin=0;
   rep(i,0,n){
  if(s[i]=='0') ans++,cnt++;
  else ans--,cnt--;
  if(i==n-1 && s[i]=='0') ccnt=max(ccnt,cnt);
  if(i!=n-1){
 if(s[i]=='1' && s[i+1]=='0' && ans<mmin) mmin=ans,cnt=0;
 if(s[i]=='0' && s[i+1]=='1') ccnt=max(ccnt,cnt);
  }
   }
   if(ccnt==0) cout<<n<<endl;
   else{
//  cout<<"min="<<mmin<<"  max="<<mmax<<endl;
  ans= ans-2*(ccnt);

  cout<<(n-ans)/2<<endl;

   }


    }
}

收获与反思

考虑单调性，维护记录值，最大/最小值。