【CSU-1581】解题报告（思维，KMP）

原始题目

Problem H: Clock Pictures

1581: Clock Pictures

  • Time Limit: 3 Sec
  • Memory Limit: 128 Mb
  • Submitted: 322
  • Solved: 82

Description

You have two pictures of an unusual kind of clock. The clock has n hands, each having the same length and no kind of marking whatsoever. Also, the numbers on the clock are so faded that you can’t even tell anymore what direction is up in the picture. So the only thing that you see on the pictures, are n shades of the n hands, and nothing else.

You’d like to know if both images might have been taken at exactly the same time of the day, possibly with the camera rotated at different angles.

Given the description of the two images, determine whether it is possible that these two pictures could be showing the same clock displaying the same time.

Input

The first line contains a single integer \(n\) \((2 ≤ n ≤ 200 000)\), the number of hands on the clock.

Each of the next two lines contains n integers \(a\_i\) \((0 ≤ a\_i < 360 000)\), representing the angles of the hands of the clock on one of the images, in thousandths of a degree.

The first line represents the position of the hands on the first image, whereas the second line corresponds to the second image. The number \(a\_i\) denotes the angle between the recorded position of some hand and the upward direction in the image, measured clockwise. Angles of the same clock are distinct and are not given in any specific order.

Output

Output one line containing one word: possible if the clocks could be showing the same time,impossible otherwise.

1.jpg
1.jpg

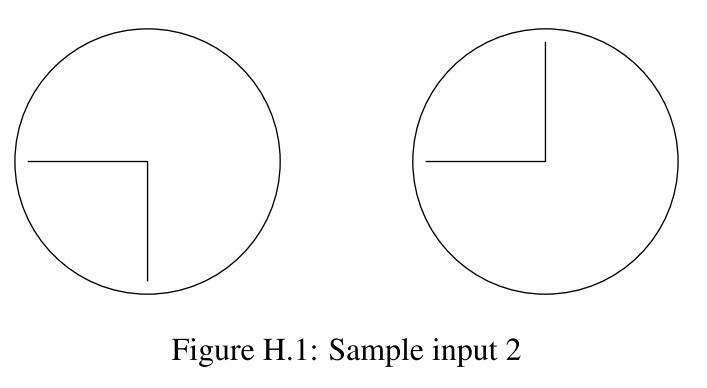
Sample Input

6
1 2 3 4 5 6
7 6 5 4 3 1

Sample Output

impossible

HINT

题目大意

  • 一个有\(n\)个指针的表盘，看不清数字，以随机顺序给出n个指针相对记录位置（不固定）的顺时针旋转角度，问两个表盘经过旋转是否能够重合（是否表示一个表盘）。

解题思路

  • 对于相同表盘，记录位置不固定，但是两个指针间的角度差固定，判断位移后可不可以相同。
  • 注意第一个指针和末尾指针的角度差需要补3600000
  • 将一组倍长做KMP可以解决这个问题，若位移后可以相同，那么倍长后2倍距离必包含另一串。

解题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
//#include <bits/stdc++.h>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <iomanip>
#include <string>
#include <map>
#include <set>
#include <algorithm>
#include <queue>
#include <vector>
#define pb push_back
#define mp make_pair
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
#define PI acos((double)-1)
#define E exp(double(1))
#define K 1000000+9
#define rep(i,a,n) for(int i=a;i<n;i++)
#define per(i,a,n) for(int i=n-1;i>=a;i--)
#define ms(x,a) memset((x),(a),sizeof(a))
const int maxn=2e5+5; 
int nt[maxn];
int aa[maxn],bb[maxn];
int a[maxn],b[maxn];
int n;
//参数为模板串和next数组
//字符串均从下标0开始
void kmpGetNext(int *s,int *Next)
{
    Next[0]=0;
//    int len=strlen(s);
    for(int i=1,j=0;i<n;i++)
    {
        while(j&&s[i]!=s[j]) j=Next[j];
        if(s[i]==s[j]) j++;
        Next[i+1]=j;
    }
//    Next[len]=0;
}
int kmp(int *ss,int *s,int *Next)
{
    kmpGetNext(s,Next);
//  调试输出Next数组
//	int len=strlen(s);
//	for(int i=0;i<=n;i++)
//		cout<<Next[i]<<" ";
//	cout<<endl; 

//    int ans=0;
//    int len1=strlen(ss);
//    int len2=strlen(s);
    for(int i=0,j=0;i<2*n;i++)  //倍长 
    {
        while(j&&ss[i%n]!=s[j])j=Next[j];
        if(ss[i%n]==s[j]) j++;
        if(j==n){
			return 1;
		}
           
    }
	return 0;
}

int main(void)
{
	ios::sync_with_stdio(false);
    while(cin>>n)
    {
    	memset(a,0,sizeof(a));
    	memset(b,0,sizeof(b));
    	rep(i,0,n) cin>>aa[i];
    	rep(i,0,n) cin>>bb[i];
    	sort(aa,aa+n);
    	sort(bb,bb+n);
    	rep(i,0,n-1){
    		a[i]=aa[i+1]-aa[i];
    		b[i]=bb[i+1]-bb[i];
		}
		a[n-1]=360000+aa[0]-aa[n-1];
//		rep(i,0,n) cout<<a[i]<<" ";
//		cout<<endl;
		b[n-1]=360000+bb[0]-bb[n-1];
//		rep(i,0,n) cout<<b[i]<<" ";
//		cout<<endl;
    	if(kmp(a,b,nt))
    		cout<<"possible"<<endl;
    	else cout<<"impossible"<<endl;
    }

    return 0;
}

收获与反思

  • 仔细读题，分析题目
  • 倍长KMP可以判断自身位移的情况。