密码技术学习——Keccak一轮破解论文整理

概述

文章给出一种对 Keccak-512 进行原像攻击的方法，该方法仅需要解 384 个线性方程组。该方法基于散列值和消息位之间方程的自由度？？（原文是：degree of freedom in threequations between hash values and message bits）。使用此方法，我们可以以恒定复杂度解位长度小于 1024 的消息对应的散列值。

Keccak 结构

Pass

注意表示方法：

  1. row: 行，长度为 5，表示 yz 确定的沿 x 轴的 5 位块。
  2. column: 列，长度 5，表示 xz 确定的沿 y 轴 5 位块。
  3. lane: 道，长度 64，表示 xy 确定的沿 z 轴 64 位块。

预先结论发现

Observation 1

在\(\chi\)运算中，对于已知密文序列，可以直接逆运算明文序列。

\[a_i = b_i \oplus (b_{i+1} \oplus 1) \cdot (b_{i+2} \oplus (b_{i+3} \oplus 1) \cdot b_{i+4})\]

Observation 2

在\(\chi\)运算中，任意非相邻三位的值已知，所有输出可以写成输入的线性组合形式。

Observation 3

对于\(a_3=1\)，可给出\(a_0,a_1,a_2\)的线性构造式，带入 Observation 1，正确。

实际上不是特质\(index = 3\)的位置，把文中公式换做\(n+3\)的表述形式应为。

条件：\(a_{n+3} = 1\)，模 5 条件下，\(0 \le n \le 4\)。

\[a_{n+2} = b_{n+2}\]

\[a_{n+1} = b_{n+1} \oplus (b_{n+2} \oplus 1)\]

\[a_n = b_n \oplus (b_{b+1} \oplus b_{n+2} ) \cdot b_{n+2}\]

该性质还会在二轮破解的文章中见到（相同作者）。

Observation 4

由\(d_0,d_1,d_2,d_3,d_4\)表示一个 column 上的四个数，那么\(CP\)值（parity of column，主要应用于\(\theta\)运算）可由\(d_i\)异或和表示。

主要跟\(\theta\)运算子有关。

简述攻击过程

  1. 关注哈希值前 8 lane
  2. 由于\(\iota\)运算实际参与的只有(0,0) lane，\({\iota}^{-1}\)只需要再跟 \(RC\)进行 \(XOR\)
  3. 将上述结果进行\(\chi^{-1}\)运算（根据 Observation，逆运算为代数 3 次），记为状态\(I\)。
  4. 根据 Observation 对 Message Block 进行处理试图达到状态\(I\)。
  5. 根据限制条件列出线性方程，如果方程独立，可解。

疑惑解答

\(d_i\)含义改变

这里首先要注意的是，\(d_i[k]\)与之前 Observation 4 中的\(d_i\)含义不一样！！

这里\(d_i[k]\)表示的是\(\theta\)运算中\(A[x][y][z]\)要异或的整体部分，其中指代关系为\(i \rightarrow x\)，\(k \rightarrow z\)。（Observation 中\(d_i\)的\(i\)表示 column 中第几个）。我们再写一下公式（以英文文献中的符号为准）。

\[d_i[k] = CP[i-1][k] + CP[i+1][k-1] \tag{1}\]

其中\(CP\)表示 column parity，公式表示为。

\[CP[x][z] = A[x][0][z] \oplus A[x][1][z] \oplus A[x][2][z] \oplus A[x][3][z] \oplus A[x][4][z]\]

\[CP[x][z] = \sum_{j=0}^{j=4} A[x][j][z] \tag{2}\]

而\(\theta\)运算实际为

\[\theta: A'[x][y][z] = A[x][y][z] \oplus \sum_{y'=0}^{y'=4} {A[x-1][y'][z]} \oplus \sum_{y'=0}^{y'=4} {A[x+1][y'][z-1]} \tag{3}\]

将 2 式带入 3 式得到

\[\theta: A'[x][y][z] = A[x][y][z] \oplus CP[x-1][z] \oplus CP[x+1][z-1] \tag{4}\]

将 1 式带入 4 式（改变一下 d 的表示）得到

\[\theta: A'[x][y][z] = A[x][y][z] \oplus d[x][z] \tag{5}\]

显然，根据含义\(d[x][z]\)至于\(x,z\)有关，同 column 下不同位置对应的值相同，这就解释了为什么后文 Fig.3 Fig.4 等配图中同一列异或相同\(d_i\)，这里的\(i\)表示 x 轴的偏移距离。So，我们可以理解作者给出的运算结果表示，如下图。

Keccak_1round_1
Keccak_1round_1

\(\theta\) Identity 含义

实际上Identity表示\(\theta\)变换为恒等变换。也即

\[A = \theta A \]

根据 Observation 4 和（2）式，xz 坐标相同对应的一个 column，所以在\(\theta\)运算中，异或的是相同的 CP 值。我们可以构造\(\theta\)运算前的特定 Cube State，使得每一个 CP 异或和为 0，这样\(\theta\)运算就是恒等的。

\[CP[x][z] = 0\]

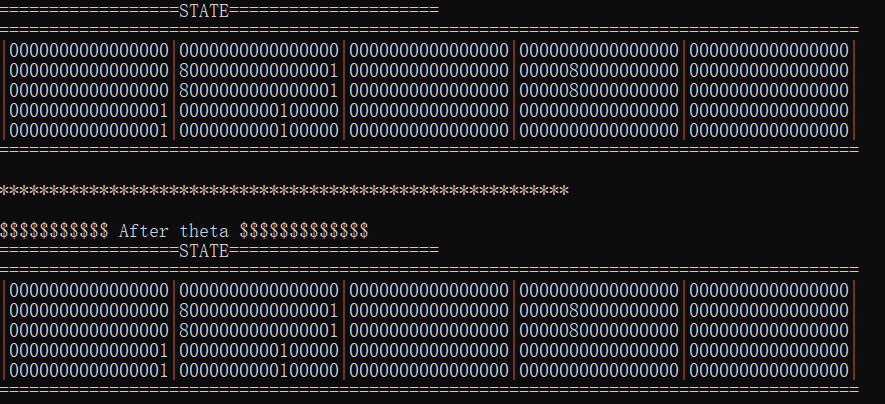
Keccak_1round_2
Keccak_1round_2

如上图

NIST SHA3 Padding 规则

Keccak 在这里使用的 Padding 方式为多重位速率填充（Multi-rate Padding），即 padding 10*1 ，至于为什么，Keccak Team 是这么解释的。

Using multi-rate padding causes each member of the Keccak family (and in particular for each value of the capacity) to act as an independent function.

注意，整除\(r\)时（恰好填满），并非不需要 padding，而是新填充一个首位为 1，中间为 0 的块

Keccak_1round_3
Keccak_1round_3
Keccak_1round_4
Keccak_1round_4

几种特殊情况（r 表示 rate 长度）

最后一个 block 长度 当前 block 填充结果 下一 block 填充结果
其他 XX...XX10001 无
r-2 XX...XX11 无
r-1 XX...XXX1 00...01
r XX...XXXX 10...01

正式攻击过程

原作者给出了单/双，Identity/Without Identity，四种情况下一轮攻击方法，在我们团队实现的一轮 Keccak-256 攻击中，我们均保证\(\theta\)运算 Identity，对单 Message Block 和双 Message Block 进行研究，达到的最好成过分别为192和256位置，双 message 的攻击已经达到 Keccak-256，n=1 的最好攻击成果（Hash 值全为 0）。

Keccak_1round_5
Keccak_1round_5

单 Message Block+ Identity

达成最好结果：192 位前缀 0

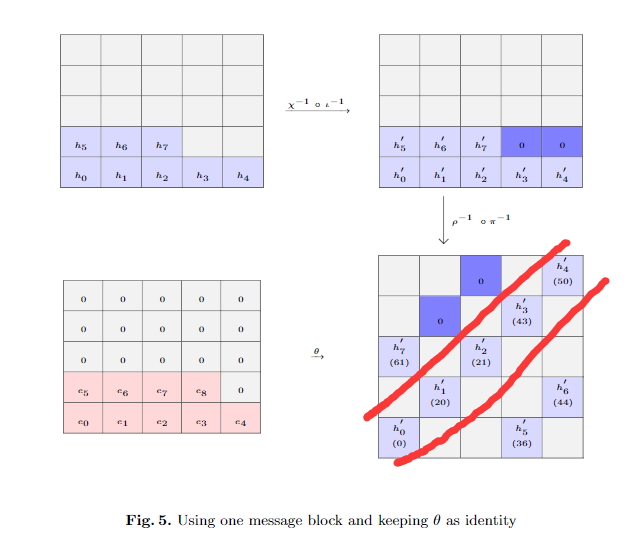
Keccak_1round_6
Keccak_1round_6

输入输出差异：赛题输入\(r=1088\)而 paper 中\(r=576\)，所以我们实际可控的输入到\(e[16]\)，且赛题输出为\(256\)位，而 paper 输出为\(512\)位。所以我们只关注\(h_0,h_1,h_2,h_3\)。

根据\(\chi^{-1}\)与\(\iota^{-1}\)运算性质，我们知道\(h'\)可用\(h\)得到，且结果唯一。\(h_0',h_1',h_2',h_3'\)经\(\pi^{-1}\)的换道与\(\rho ^{-1}\)的 z 轴移动，我们发现道排布在\(y=x\)对角线上，对应输入位置得到。

\[h'[0] = e[0]\] \[h'[1] = e[6]\] \[h'[2] = e[12]\] \[h'[3] = 0\]

在\(h'[3]\)要全为\(0\)的限制下（在容量 c 中，不在可异或的 r 中），我们团队尝试构造最好的 Hash 串为\(h[3][0]=1\)，其余位置均为\(0\)，如此前缀长度为\(192\)，根据条件构造输入，代码：

1
2
3
4
5
6
7
8
9
for (int i = 0; i < 64; ++i) {
    e[0][i] = hh[0][i];  // e_0 e_5  e_10  e_15
    e[5][i] = hh[0][i];
    e[10][i] = hh[0][i];
    e[15][i] = hh[0][i];
}

//for padding
e[11][0] = e[11][63] = e[16][0] = e[16][63] = 1;

在验证程序中输入长度为\(1024\)，验证程序自动 padding（和我们上面的\(e_16\)赋值相同），\(e_{11}\)用来对冲\(e_{16}\)从而保证\(\theta\)的恒等性质。

双 Message Block + Both Identity

达成最好结果： 256 位前缀 0

容易忽略的问题：\(\rho\)运算带来的 z 轴偏移，

完成单 Message block 的情况下，我们思考是什么导致了\(h_3\)的限制，实际上是由于初始 State，除 r 长度内可通过输入长度，其他位置均为 0，因此倒推过程中我们必须满足\(h'_3=0\)。

不过经过一个 Message 的轮转后，其他位置不再是固定的 0 值了，我们的想法：通过构造第一个 Message D 使\(h_0'h_1',h_2'h_3'\)达到一个合适状态\(F'\)（使得经最后两运算子后\(F = (\iota \circ \chi) F\)），\(F\)全为 0，即\(h_0h_1h_2h_3\)均为 0。

构造细节，注意 Z 轴偏移（正偏反偏），代码：

Message D

1
d[4][(64 - 27 + 43 + 64) % 64] = d[9][(64 - 27 +43 + 64) % 64] = d[1][64 - 45] = d[16][64 - 45] = 1;

再进行第二消息 Message E 的构造，目标有三个：

  • 保持第二轮\(h_3'\)位置的状态位置
  • 斜线（影响 hash 值）异或指定值达到\(F'\)
  • 其他地方补 1 达到纵列\(CP\)值为 0，使\(\theta\)恒等

代码：

Message E

1
2
3
4
5
6
7
8
9
10
11
12
// x=0
e[5][0] = e[10][20] = e[15][43] = 1;
// x=1
e[6][36] = e[6][0] = e[6][20] = 1;
e[1][20] = 1;
e[11][0] = e[11][63] = 1;
// x=2
// pass
// x=3
e[8][0] = e[13][20] = e[13][43] = 1;
// x=4
e[9][36] = 1;