Step 1

题目摘要引言

摘要

摘要：基于先驱们的方法（Aumasson Meier 和 Dinur），本问分析了 Round-Reduced 情况下的 Keccak 函数家族安全性。介绍了一种新的工具linear structure用于线性化至多 3 轮的 Keccak 轮转函数置换。该工具的直接应用是在不增加复杂性的条件下衍生出两轮的zero-sum distinguishers。结合 S 盒性质、双线性结构知识，应用该结构于至多 4 轮的 Keccak 原像攻击。

现有分析还不足以影响 Keccak 算法的安全性。

贡献

1. 利用零和区分器找到 Permutation 的输入。该零和去分离利用了低代数度（2/3）下 S 盒的性质。（存疑）攻击从排列的中间开始，并自由地向排列的前后两个方向扩展。本文中的linear structures拓展了轮次，并且结合 Keecak-f 的 S 盒性质，增加了可应用的 attack rounds（在不增加复杂度的情况下）。
2. 文章的第二个贡献是改进了原像攻击方法，与之前使用的 meet-in-the-middle和 SAT求解器 相比。通过线性化技术，将求原像问题转化为求解线性方程组问题。（！！！可以应用）三轮原像攻击的复杂度被大大降低，因而使文章团队能够找到 SHAKE128（Keccak[r = 1344, c = 256] 和我们的 Keccak256 非常相似）。

攻击复杂度总结

Keccak_2round_1

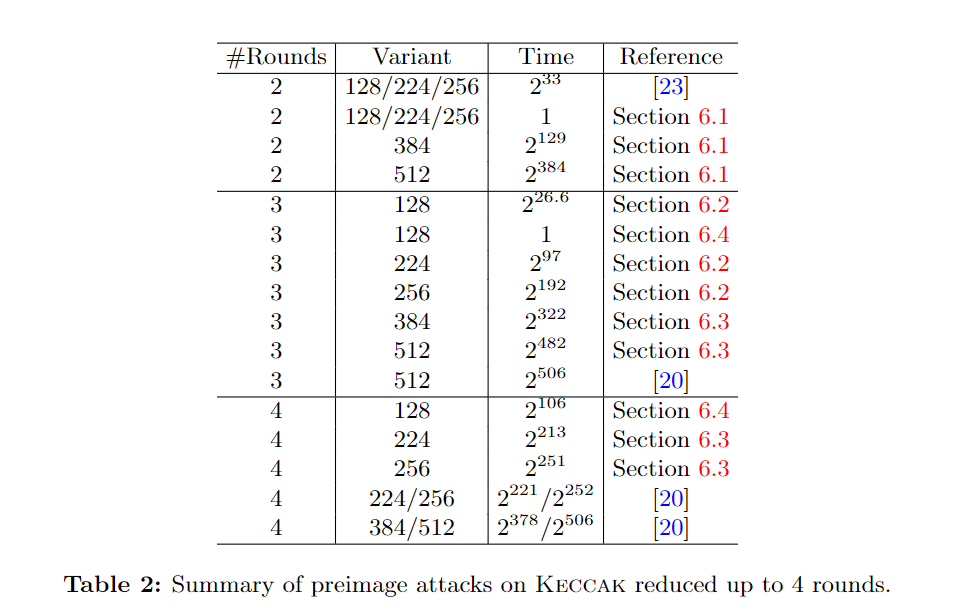
基本理论概况

结论部分

介绍并描述linear structures。构造理论上至多 15 轮（可实现 11 轮）的 Keccak-f 上的零和区分器。

进一步优化低轮原像攻击的复杂度，通过解一次线性方程组计科求得 2 轮 Keccak-224/256, 3 轮 SHAKE-128 的原像。

It will be interestring to see applications of linear structures to other Keccak-like ciphers and functions.

回答基本问题

1. 类别

   对 Keccak 原型密码系统分析，提供新的攻击方式，

2. 内容

   1 轮相关，发现\(\chi\)及其逆运算\(\chi^{-1}\)类似性质。Zero-Distinguisher 没有接触过，可能需要补充阅读。

   理论基础：Keccak-f[1600] S 盒性质，零和区分器，线性代数。

3. 正确性

   被许多 Round-Reduced 攻击的论文引用，正确且有效。

4. 创新点

   提出linear stucture结构，对 Round-Reduced 低轮模式进行线性化。

1. 清晰度

阅读选择

较多相关文献都提到了该文章，有继续深入学习的必要

Step 2

细读笔记

二轮破解已经实现，故忽略

4.2 节，如何使三轮仍保证线性

在 two rounds 后仍保证线性，我们令\(A[i,j] \quad with \quad i=0,2 \quad and \quad j = 0,1,2\)。

为保证变量在第二轮\(\theta\)运算后不扩散，我们多了三组（每组 64 个）方程限制，这时需要对经过第一轮旋转和纵向移位的小块做 limit。

解释 To ensure

问题记录

未读（且值得读）文献记录

Aumasson, J.P., Meier, W.: Zero-sum distinguishers for reduced Keccak-fand for the core functions of Luffa and Hamsi.

Step 3

思路复现

证明与推理复现

实验验证复现

为何二轮攻击最后需要求补

\(\rho\)运算赋值，赋值是 A[x][z] <- A[x][z-t]， 新的z的位置，所有的运算停留在\(z=0\)截面上，

第三轮

\(h'0 = h'1 = h'3 = RC\)