机器学习——复习大纲
题型
- 一定会考的:决策树,神经网络,过拟合,集成学习
- ppt 提出的问题会以选择题形式考察
- 不会考数学推导和证明
必须要带计算器!
12.31(周二)下午 4-5 点半。B206
Chap1 基本概念
基本术语:属性,属性值,属性空间,训练样本,测试样本
监督学习与非监督学习
区别,给出一个问题确定是哪种问题类型。分类和回归,分类和聚类。 标签的问题。
李:
!!线性判别分析,两类现行判别分析,内部方差,中心距离 !!如何求判别线
Chap2 线性模型
归一化
- 特征尺度归一化(确保特征在相同的尺度)
- 范围归一化:使得每个特征尽量接近某个范围,如\(0 \le x_i \le 1\)
- 零均值归一化:用\(x_i - \mu_i\)替代\(x_i\),即\(x_i - \mu_i \rightarrow x_i\),其中\(\mu_i = \frac{1}{m} \sum_{i=1}^m x_i\)
- 零均值+范围归一化,如\(-0.5 \le x_i \le 0.5\)
- 零均值单位方差归一化:\(\frac{x_i - \mu_i}{\sigma_i} \rightarrow x_i\)
机器学习三要素
- 模型、策略、算法?
- 数据、模型、算法?哪个对
线性模型基本形式
\[f(x) = w^{T}x+b = \theta^T x\]
两种表示,注意前式中带偏秩,但是并不表达在矩阵相乘中。
\[J(\theta) = \frac{1}{2m} \sum_{i=1}^{m} (h_\theta (x^{(i)}) - y ^{(i)})^2\]
求解损失函数最小值,梯度下降方法为常见方法之一,梯度下降只能达到局部最优,凸函数可以达到全局最优。
- 什么是线性关系、
- 一元线性回归,损失函数相关,最小化损失函数。
- 梯度下降法,梯度的方向。
- 欠拟合、过拟合。
学习率
- 怎样确保梯度下降算法正确的执行(收敛性)
- 自动收敛测试:每次迭代损失函数\(J(\theta)\)是否减少
- 收敛条件:定义不再进行迭代的收敛阈值(如\(10^{-3}\))
- 怎样选择学习率\(\alpha\)
- 对于足够小的\(\alpha\),\(J(\theta)\)应该在每一次迭代中减少
- 如果\(\alpha\)太小,梯度下降算法则会收敛很慢
- 如果\(\alpha\)太大,梯度下降算法则不会收敛:发散或震荡
- 用户可以以非常低的学习率开始训练模型,在每一次迭代过程中逐渐提高学习率(线性提高或者指数提高都可以),用户可以用这种方法估计出最佳学习率。
改进方法
- 正规方程(The normal equations)
- 对于求函数极小值问题,令函数微分为零,然后求解方程(而非每次对梯度递减)可得到解析解
- 西瓜数 P54 P55
现在使用的梯度下降为批量梯度下降(BGD),每次需要计算所有的样本(1->m),可以采用随机梯度下降(SGD)(随机选取一个样本,伪梯度下降)
梯度下降的改进方法
动量法
动量法是一种非常简单的改进方法,已经成功应用数十年。动量法的核心思想是:在梯度方向一致的地方加速,在梯度方向不断改变的地方减速。
- 在下降初期,使用前一次的大比重下降方向,加速。
- 在越过函数谷面时,异常的学习率,会使得两次更新方向基本相反,在原地“震荡” 此时,动量因子使得更新幅度减小,协助越过函数谷面。
- 在下降中后期,函数面局部最小值所在的吸引盆数量较多,一旦陷进吸引盆地当中,梯度趋于零,会导致止步不前,学习无法进行。如果有动量项的话,动量因子使得更新幅度增大,协助跃出吸引盆。
NAM
略
Chap3 logistic 回归
分类问题,线性模型可以通过设置阈值来达成判别。阈值选择有一点困难,因为线性模型值域 R 太广,逻辑斯特回归则希望预测函数值限制在[0,1],\(0 \le h_{\theta} (x) \le 1\)。
Sigmoid 函数的性质
\[g(z) = \frac{1}{1+ e^{-z}}\]
\[g'(z) = g(z) (1 - g(z))\]
概率解释
\[P(Y = 1 | x) = h_\theta(x) = g(\theta^{T}x) = \frac{1}{1+e^{-\theta^Tx}}\]
输入 \(x\) ,输出 \(y=1\) 的可能性
物理含义:对比线性模型的平滑过度,logistic 回归在分界值前后变化剧烈,希望达到理想的二值 Sigmoid 的函数,但由于需要合适的损失函数求解 \(\theta\) 参数矩阵,没有使用不连续的二值 Sigmoid 函数
损失函数选择
回顾凸函数,线性模型带入\(h_\theta(x) = \theta^Tx\)入平方损失函数\(J(\theta) = \frac{1}{2m} \sum_{i=1}^{m} (h_\theta (x^{(i)}) - y ^{(i)})^2\),得到的是凸函数,也可解。
- 凸函数
- 等价于 \(f''(x) \ge 0 , \forall x\)
- 若\(x\) 为矢量,则对应的条件变为 Hessian 矩阵\(H\)为半正定矩阵
- 严格凸(小于)
- 对于矢量,则对应条件变为 Hessian 矩阵\(H\)正定

可以通过极大似然估计\(\theta\),见西瓜书 P59


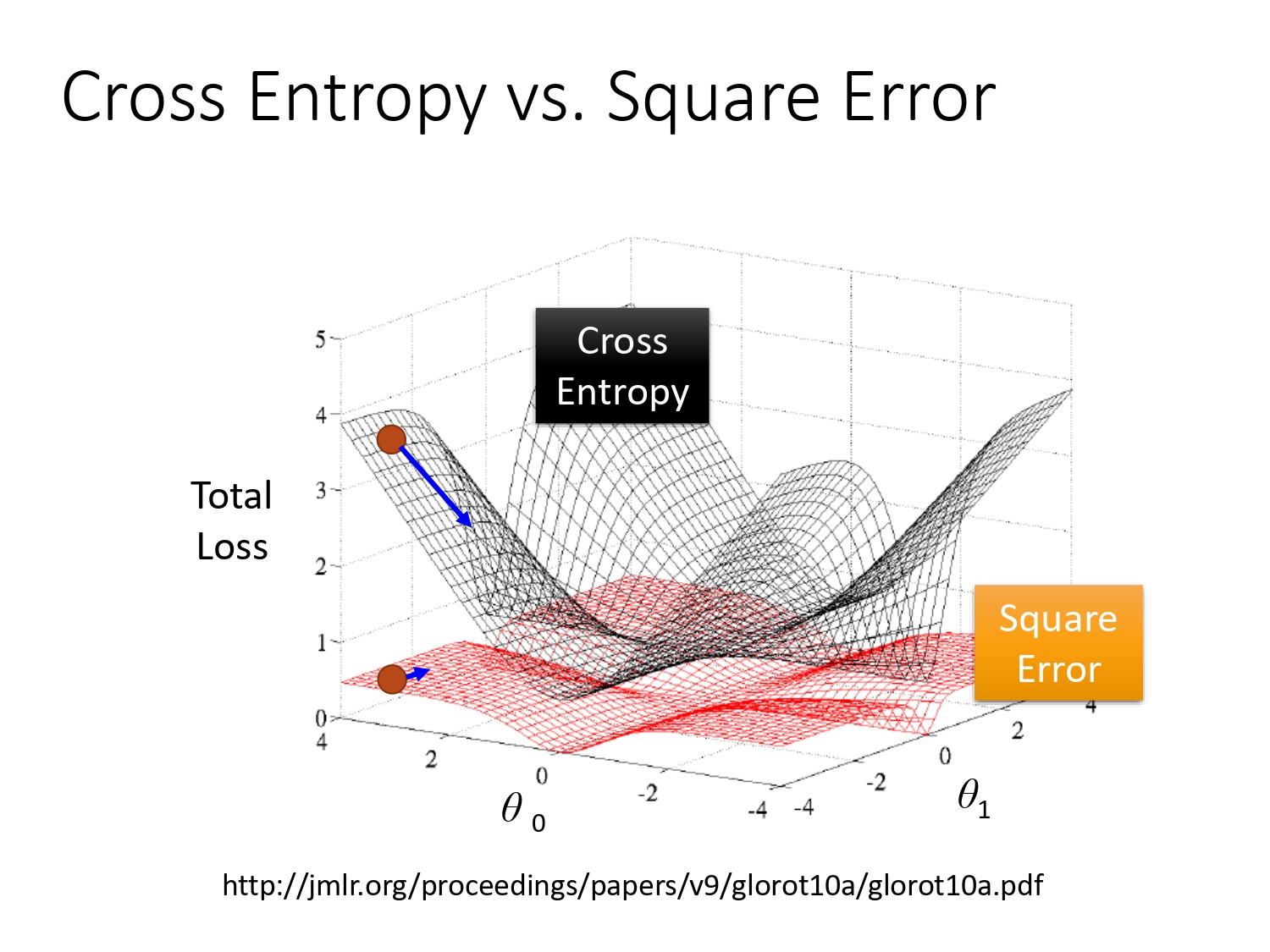
- 交叉熵损失
为什么选择交叉熵而不选择平方损失,平方损失求导中间多两项,在明确分类的两端下降率接近 0,


Chap4 过拟合和正则化
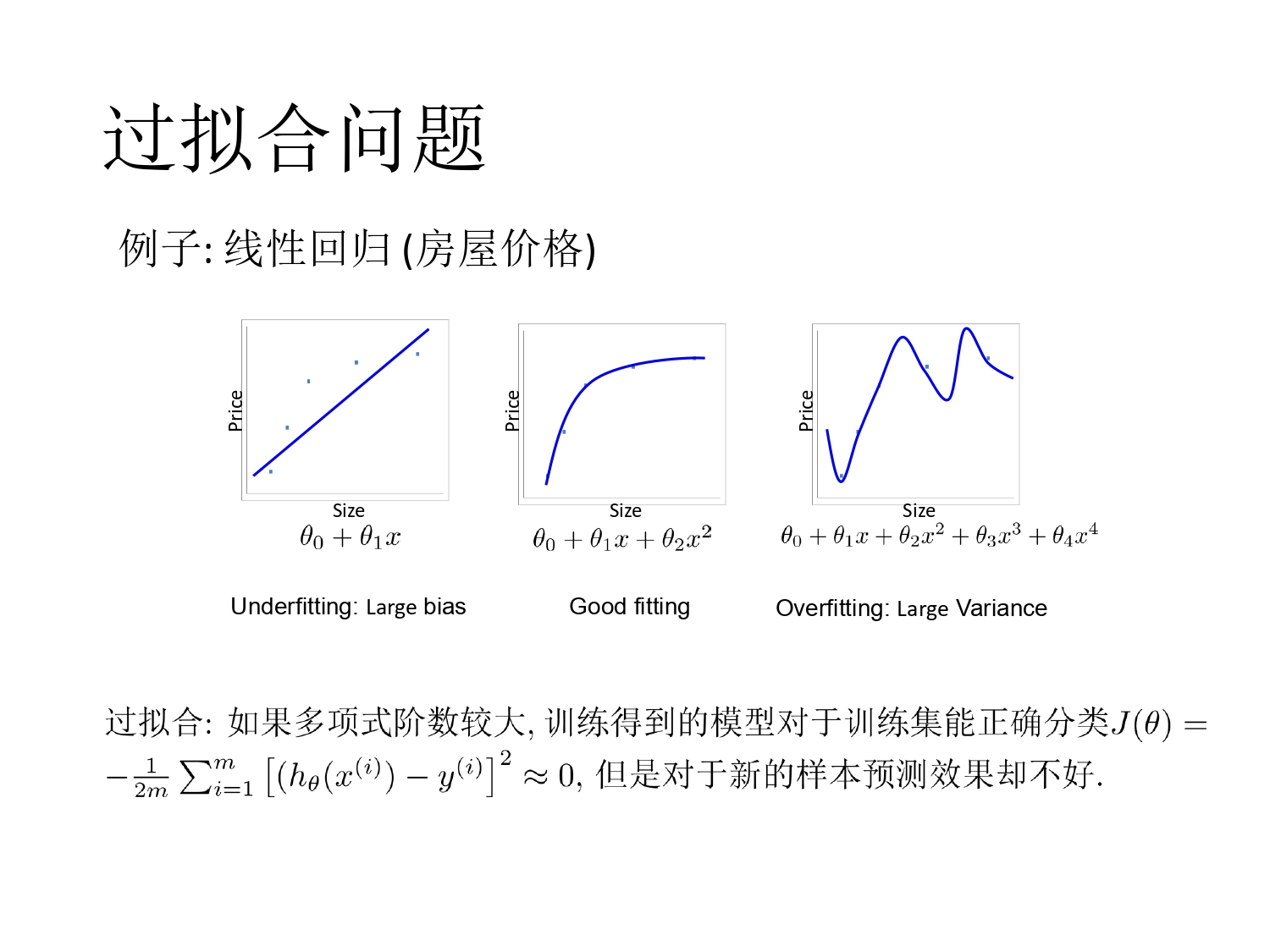
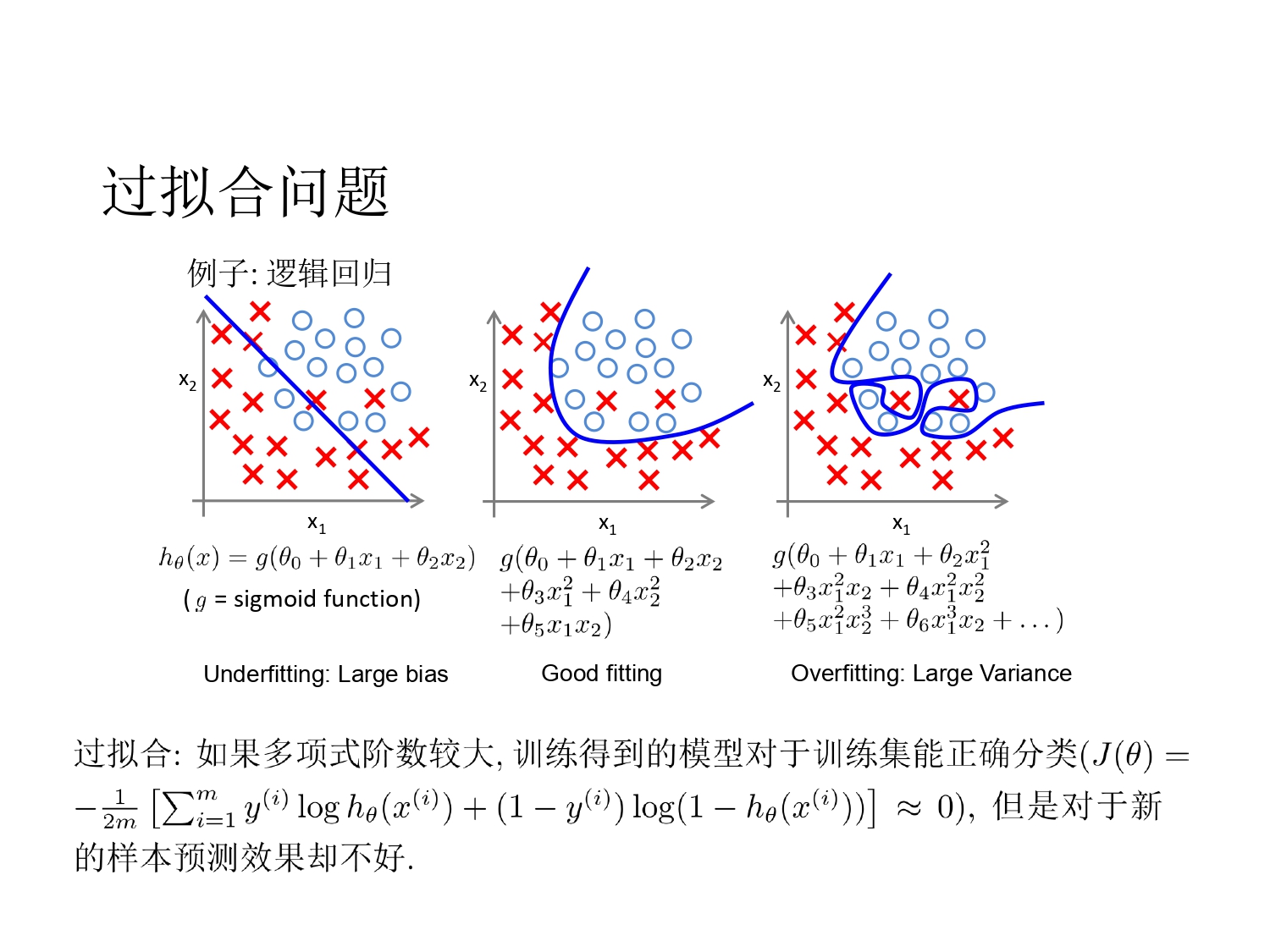
过拟合举例
为什么出现过拟合
- 最小化训练集上的损失(损失错误)
- 一般而言,模型越复杂(阶数高或特征多),训练得到的模型经验错误越低,但却更容易出现过拟合
- 选择哪个模型更合适?随机分成两部分:训练集和验证集(Validation Set)
- 训练误差和验证误差
如何判断是否出现了过拟合或者欠拟合
根据曲线判断,bias(偏差)和 variance(方差),会有 trade off(分界分离),选择靠近该分界点的模型,从而减小整体误差。
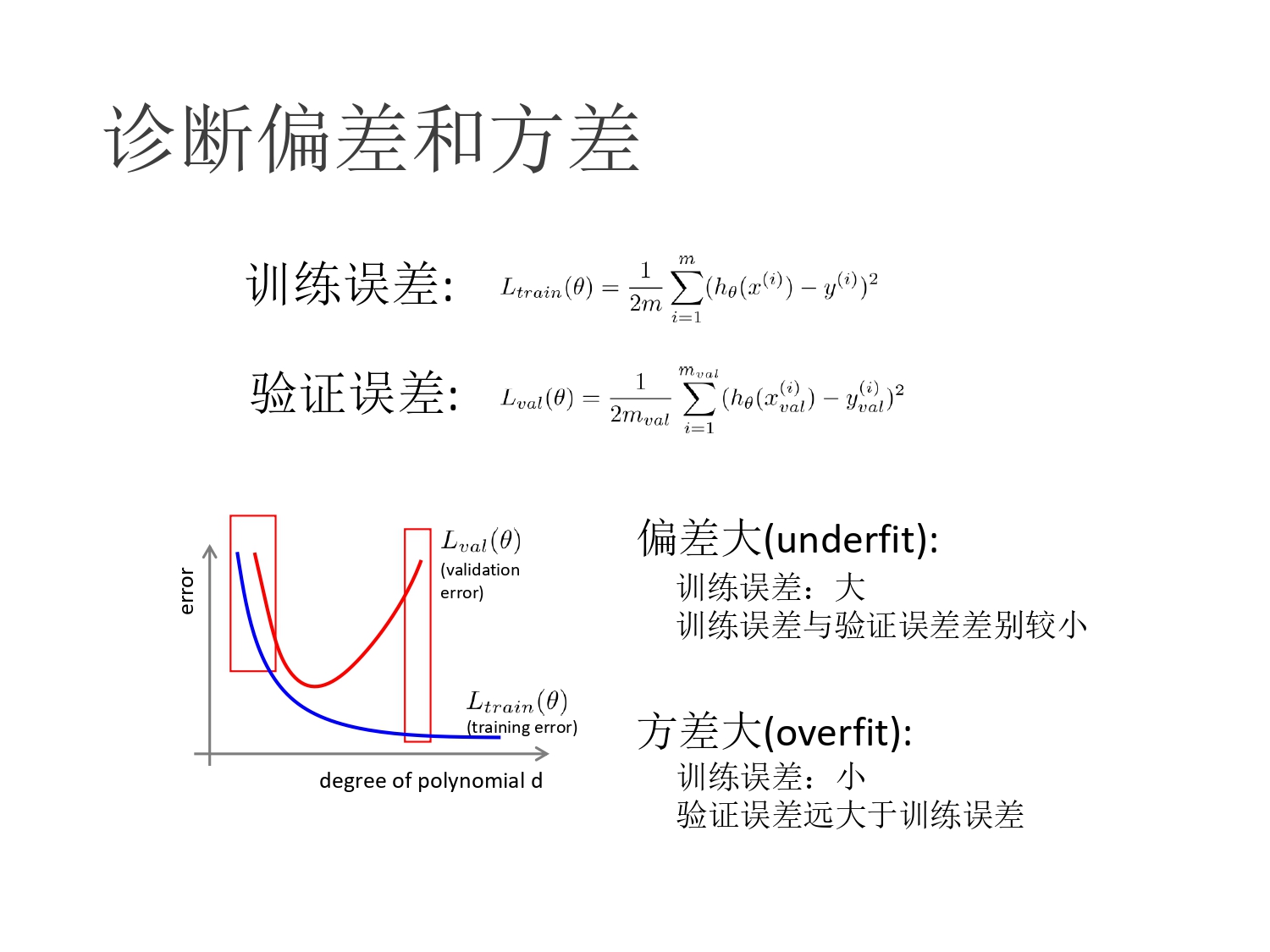
如何解决过拟合或者欠拟合问题
- 欠拟合(Large Bias):增加模型的附加都
- 收集新的特征
- 增加多项式组合特征
- 过拟合(Large Variance)
- 增加数据(有效但是实践意义不大)
- 降低模型的复杂度
- 减小特征:特征选择
- 正则化(Regularization):增加偏差
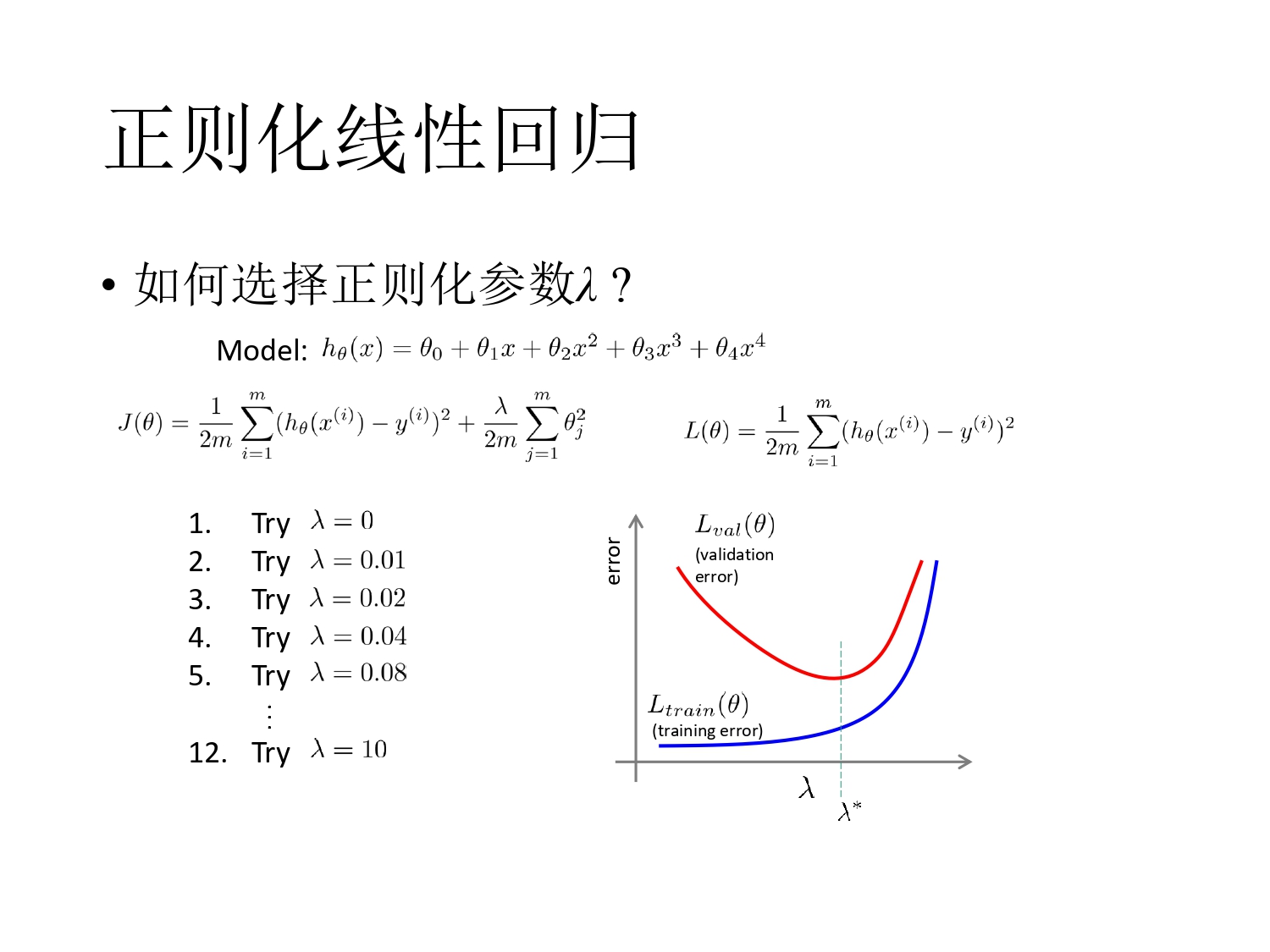
正则化
- \(\lambda\):正则化参数
- 问题:思考正则化参数的取值范围
\[\lambda \sum_{j=1}^{n} \theta_j^2\]
正则化线性回归


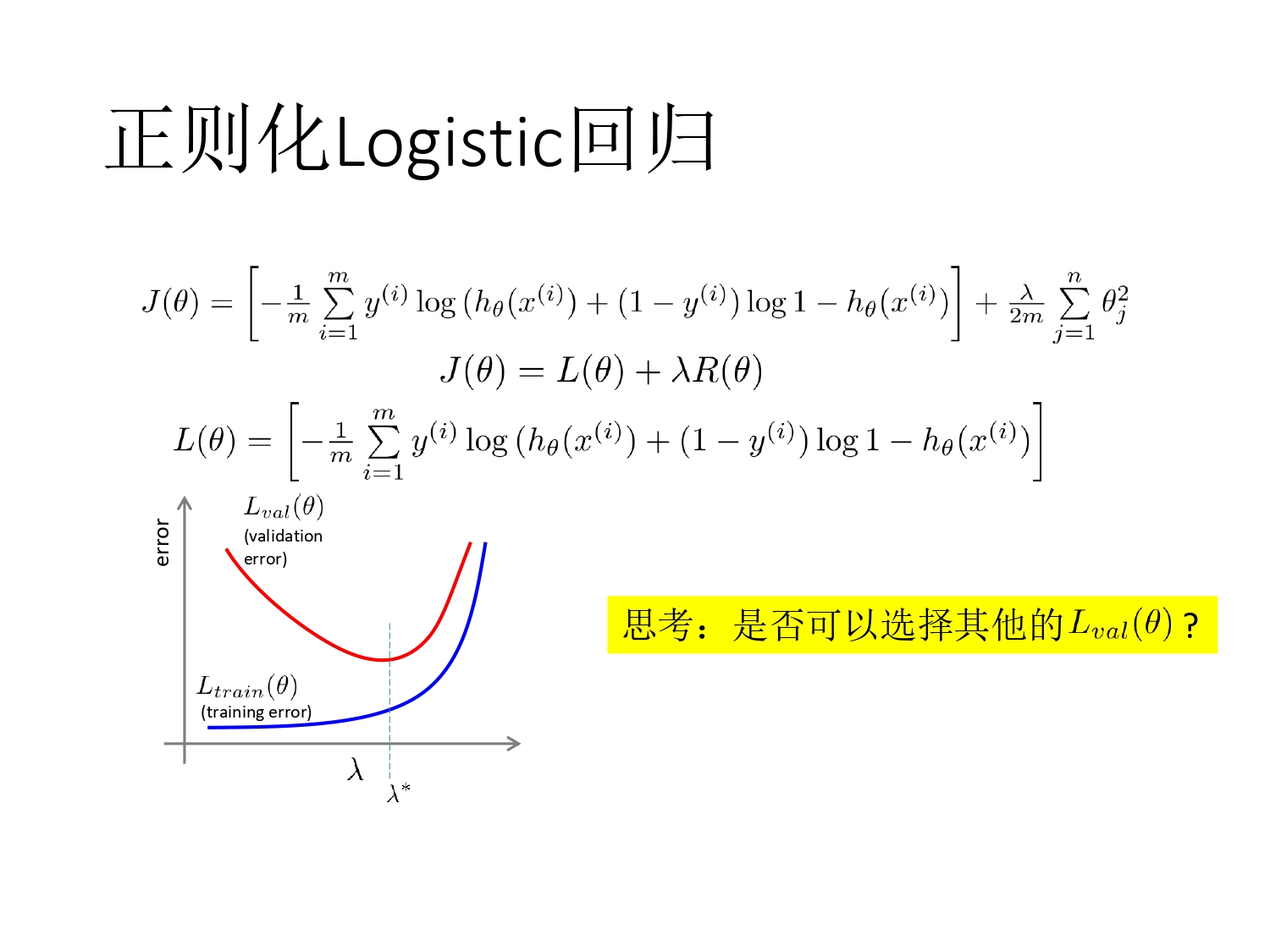
正则化 Logistic 回归

模型性能评估
- 我们用训练集优化参数\(\theta^{*} = arg min \frac{1}{m} \sum_{i=1}^{m} l(h_{\theta}(x^{(i)}),y^{(i)})\)
- 用验证集选择模型
- 但真正关心的是模型在新的测试数据的性能(泛化能力)
- 训练集:训练参数
- 验证集(开发集,Development set):用于调参(正规化参数、多项式阶数等)、特征选择等
- 测试集:仅仅用于性能评估


Chap5 神经网络
引入原因与神经结构
- 类比人类的学习方式,The "one learning algorithm" hypotheis。人类的学习行为都是通过神经元结构完成。
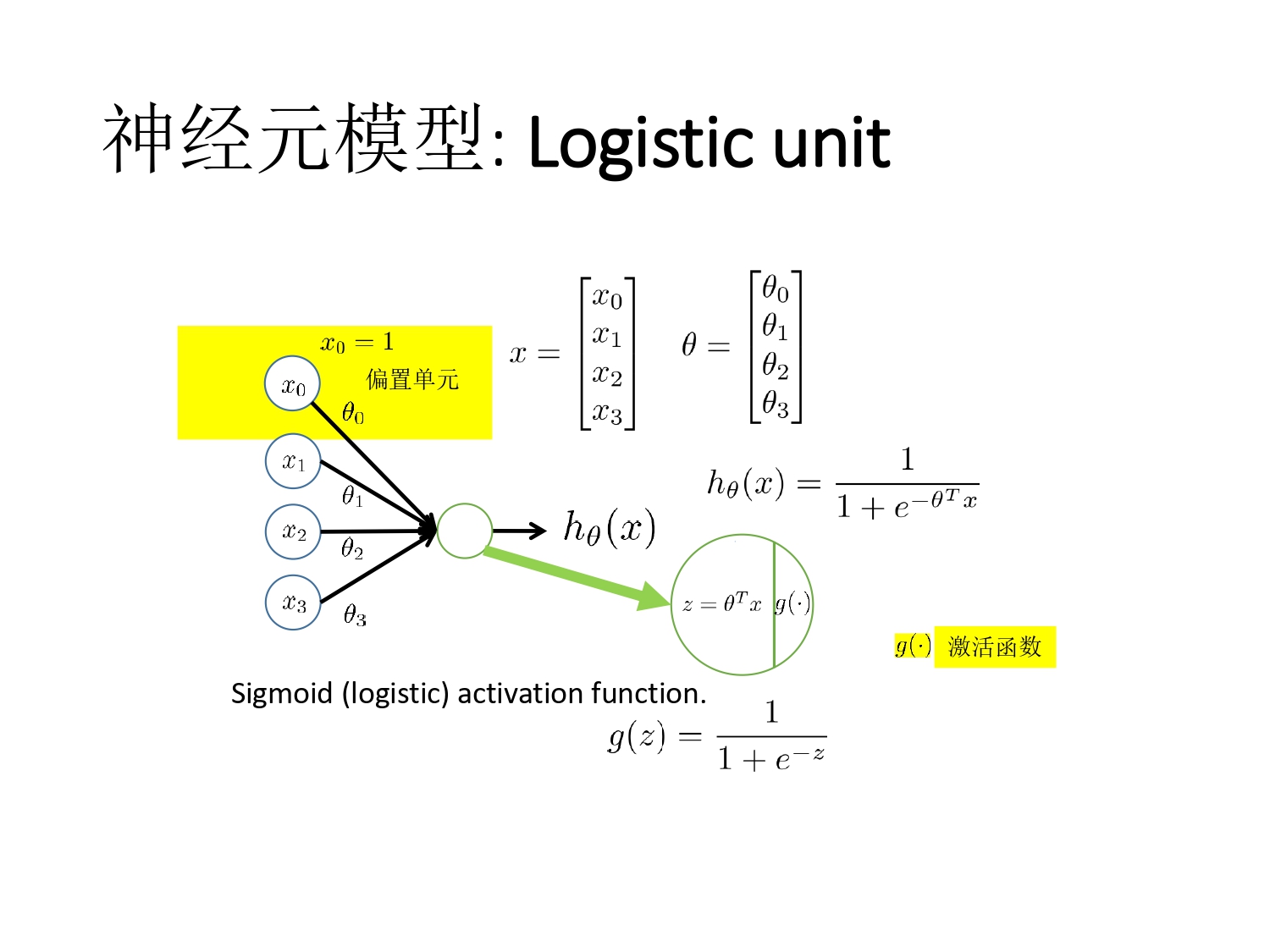
- 神经元模型:Logistic unit
神经网络结构
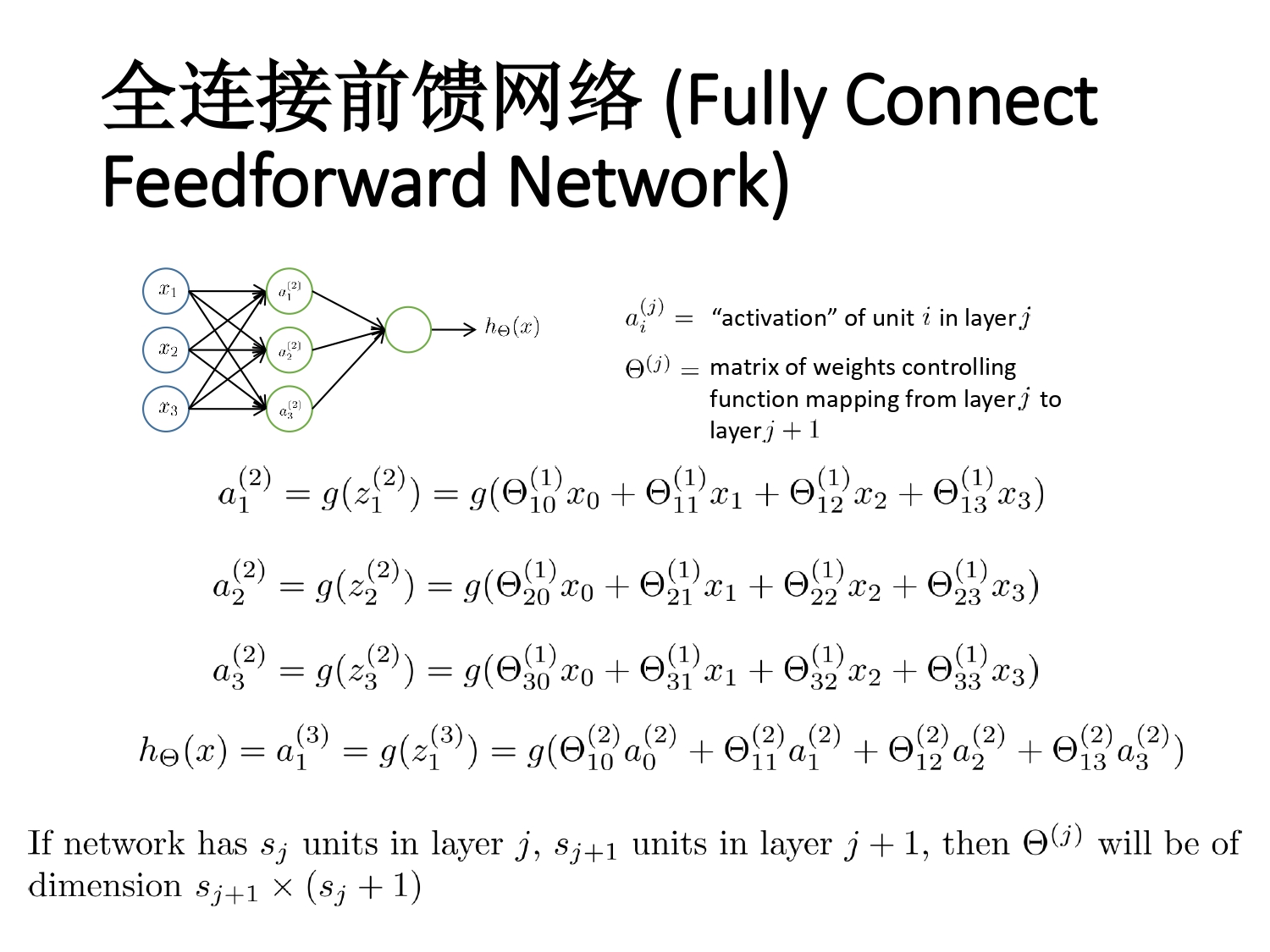
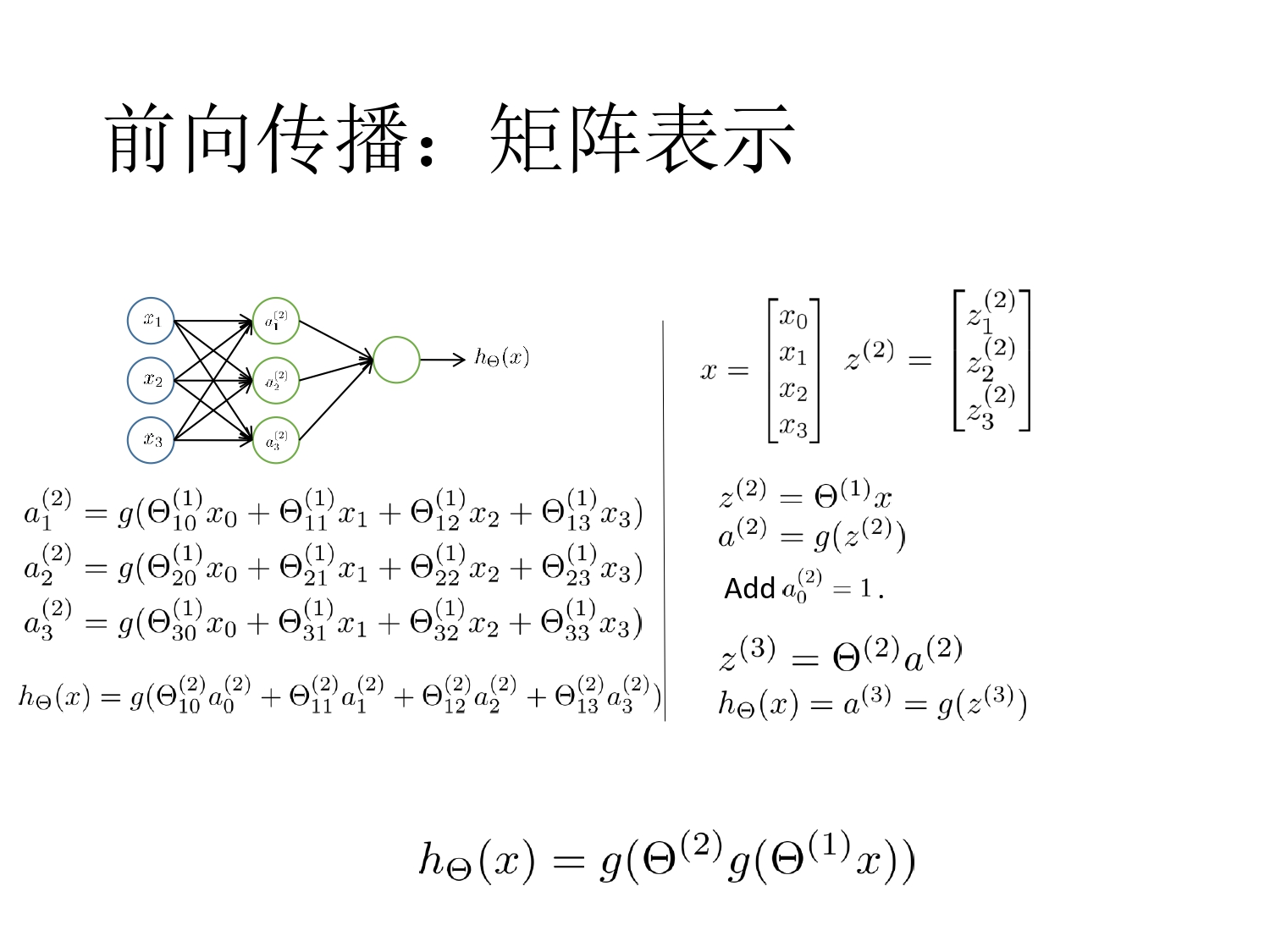
前向传播

梁:
- 为什么要引入神经网络
- 神经网络的结构
- 会算前向传播和 BP
- 多分类,softmax,交叉熵
- 掌握标准激活函数,特点
- 掌握各种方法更新梯度
- 为什么不能用 0 初始化权重矩阵
李:
神经网络,损失函数,表达式!
Chap6 SVM
Margin
- 对比 Logistic 回归:在测试新样本时,当\(\theta^Tx \gg 0\),或者\(\ll 0\),我们可以非常自信地给出预测
- 按实际训练中我们不能很好的找到一个参数矩阵使得\(\theta^Tx \gg 0\),当\(y^{i} = 1\)时以及相反时候。
重新定义符号
- (不要求掌握优化推导和 SMO)
- 什么是支持向量,margin,分类面
- 给数据,算方程、画超平面
- kernel,可能会有大题
- 基本概念:
- 主问题,对偶问题,惩罚因子(分别对应对应 hard/soft SVM 去掌握)
调节 kernel 参数能够防止 SVM 出现过拟合嘛?
李:
- 支持向量、怎样求最优超平面
- 核函数相关。
Chap6.5 决策树
信息增益
- Shannon 1948 年提出的信息论理论
- 熵:信息量大小的度量,即表示随机变量不确定性的度量
- 事件\(a_i\)的信息量\(I(a_i)\)可如下度量:\(I(a_i) = -p(a_i)\log p(a_i)\)
- 假设\(n\)个两两不相容事件\(a_1,a_2, \cdots ,a_n\),它们中有且仅有一个发生,则平均的信息量(熵)可以如下度量: \(I(a_1, \cdots , a_n) = \sum_i I(a_i) = -\sum_i p(a_i) \log p(a_i)\)
- 假设当前样本集 D 中第\(k\)类样本的比例为\(p_k\),对应的信息熵为
\[Ent(D) = - \sum_k p_k \log p_k\]
- \(Ent(D)\)越小。表示数据越有序,纯度越高(一类是 0),分类效果越好
- 假设某离散属性\(a\)有\(V\)个可能值,若采用该属性对样本集划分,则会产生 V 个分支,每个分支节点包含的数据记为\(D^v\)
- 用属性\(a\)对样本集\(D\)进行划分,获得的信息增益为:
\[Gain(D,a) = Ent(D) - \sum_v \frac{|D^v|}{D} Ent(D^v)\]
- 选择具有最大信息增益的属性来划分: \(a^* = arg \quad max_aGain(D,a)\) (ID3 算法)
信息增益比
- ID3 算法以信息增益为选择属性,对于取值较多的属性有所偏好(带编号的显然不适合)
- 信息增益比
\[Gain\_ratio(D,a) = \frac{Gain(D,a) }{ IV(a)}\]
其中 IV 成为属性的固有值(intrinsic value),属性可取值越多,IV 通常越大。
\[IV(a) = - \sum_{v=1}^V \frac{|D^v|}{|D|} \log \frac{ |D^v| }{|D|} \]
- 增益率准则对可取值数目较少的属性有所偏好
- C4.5 并不是直接选择增益率最大的候选划分属性,而是使用了一个启发式算法,先从划分属性中找出信息增益高于平均水平的属性,再从中选择信息增益率最高的属性 a。
基尼指数
- 数据集的纯度用基尼值来衡量
\[Gini(D) = \sum_{k=1}^{|y|} \sum_{k' \not ={k}} p_k p_k' = 1 - \sum_{k=1}^{|y|} p_k^2\]
- 直观来说,基尼值反映了从数据集\(D\)中随机抽取两个样本,其类别标记不一致的概率,因此基尼值越小,数据集纯度越高
- 属性 a 的基尼指数定义为
\[Gini\_index(D,a) = \sum_{v=1}^{V} \frac{D^v}{D}Gini(D^v)\]
- CART vs. ID3
- 二元划分:二叉树不易产生数据碎片,精确度往往也会高于多叉树
- 属性选择不同
剪枝
决策树的剪枝减少决策树的规模(模型复杂度),是处理“过拟合”的主要手段
前剪枝
见西瓜书 P81 给出的方法,将数据集划分为训练集、测试集,每一次选出最优划分属性后,对测试集做划分前后比对,划分后精度下降的禁止划分(图 4.5 图 4.6 以及下面的文字表述)。
预剪枝基于贪心禁止分支展开,带来一定欠拟合的风险。
后剪枝
生成完整树后做替换检查,见 P83
连续与缺失值处理
连续属性处理
- 离散化,最简单的是二分法
- 本质是连续的,但是对于有限采样数据是离散的
- 对于离散区间中取任意值产生的划分结果相同
- 对于包含\(n-1\)个元素的候选划分点集合
\[T_a = \{ \frac{a^i + a^{i+1}}{2} | 1 \le i \le n-1 \}\]
- 即把区间\([a^i,a^{i+1}]\)的中位点作为候选划分点
- 处理时对多属性需要多一轮枚举循环,找到划分后纯度更高的划分点
- CART 则将这些划分点当成多离散值处理,见后面。
CART 属性取值离散超过两种的处理
- 组合的方式转化成多个二取值问题(类似 OvR),取其中划分后 Gini_index,最小的二分情况
Chap7 集成学习
- 构建多个学习器一起来结合来完成具体地学习任务
- 也成为多分类器系统
- 学习器可以是同类型地,也可以是不同类型
- 通过将多个学习器进行结合,常可获得比单一学习器显著优越地泛化性能,对“弱学习器”尤为明显
- 理论分析指出:假设各分类器地错误率相互独立,则随着集成个体分类器数目增大,集成的错误率将指数级下降
- 现实中个体学习器是为解决同一个问题训练出来的,不可能相互独立
- 如何产生并结合“好而不同”的个体学习器是集成学习研究的核心。
集成学习分类
- 个体学习器间存在强依赖关系,必须串行生成的序列化方法。代表:Boosting(AdaBoost,Gradient Boosting Machine)
- 个体学习器间不存在强依赖关系,可同时生成的并行化方法。代表:Bagging 和随机森林(Random Forest)
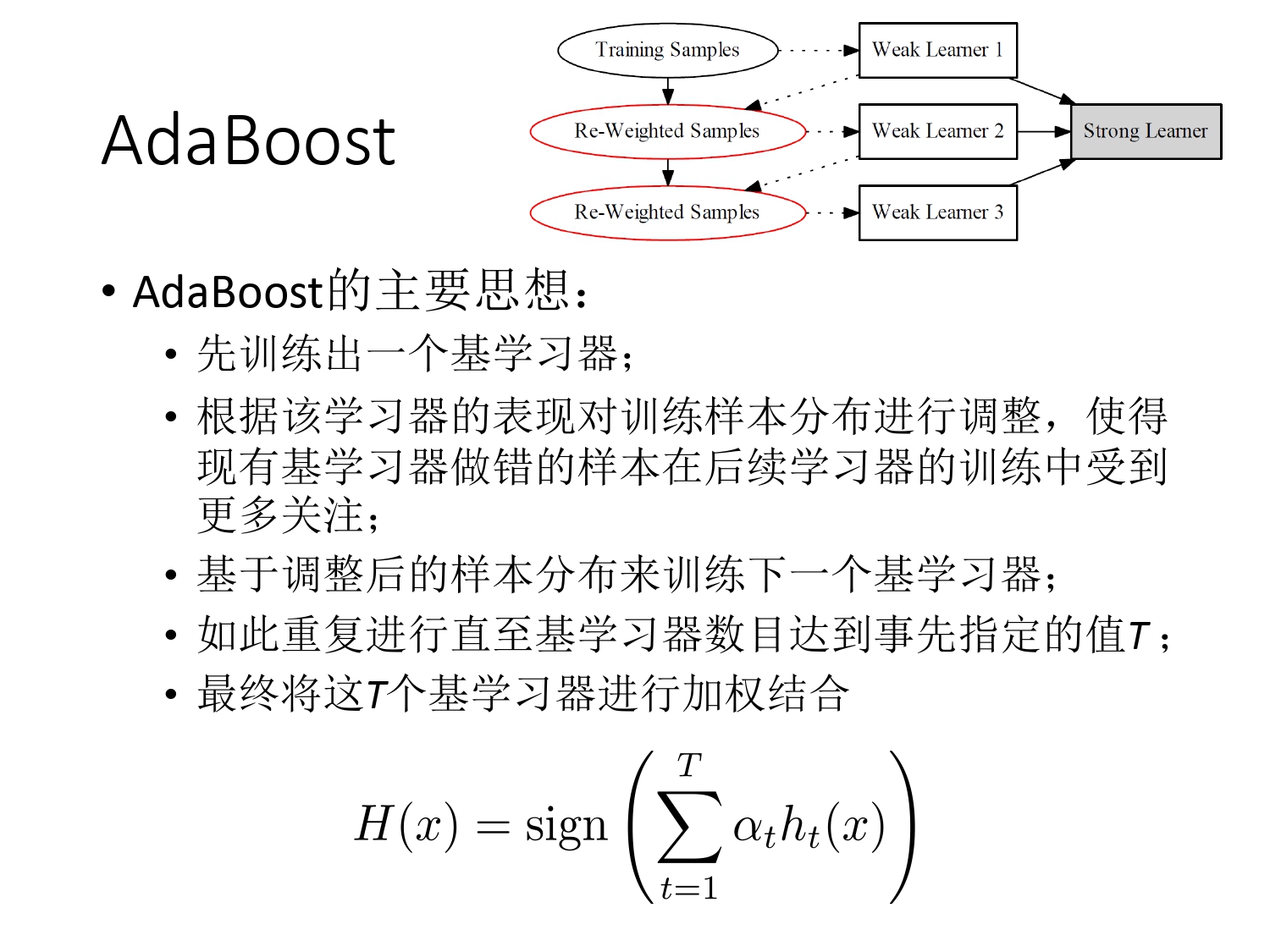
AdaBoost
李重点

GBDT
略
Bagging


随机森林(Random Forest)

决策融合策略
- 平均法
- 加权平均法
- 投票法
- 绝对大多数投票(Majority Voting):超过半数,则决策,否则拒绝
- 少数服从多数(Plurality Voting):得票最多的标记
- 学习法
- 用各学习器的输出生成新的训练数据,再去训练一个学习器(如线性 SVM 等)
Chap8 聚类
梁:
- GMM 不考
- k-means 一定考
- 高斯分布和贝叶斯系列(10')
李:
- K-means
- 以及初始类簇中心点的确认
Chap9 降维
- (流形学习不考)
- PCA/LDA 考其一
Chap10 应用
- 各种评价指标:精度等,一级二级指标
- 混淆矩阵
- ROC 曲线。Kappa 系数,AUC 值
多分类学习
多分类学习的拆解:OvO,OvR,MvM。投票机制,拆解原则。 海明距离、欧式距离。
混淆矩阵,一些指标的计算,
欠拟合的改良方法
贝叶斯
回顾概率公式,全概率公式,先验概率、后验概率
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!