数字图像处理——直方图匹配

基本概念

上一篇文章讲了直方图均衡相关内容，从实际应用中我们发现，只能对直方图做均衡操作并不能完全满足我们的需要，有时我们更希望调整概率分布（直方图）为指定形状，这就是直方图匹配。

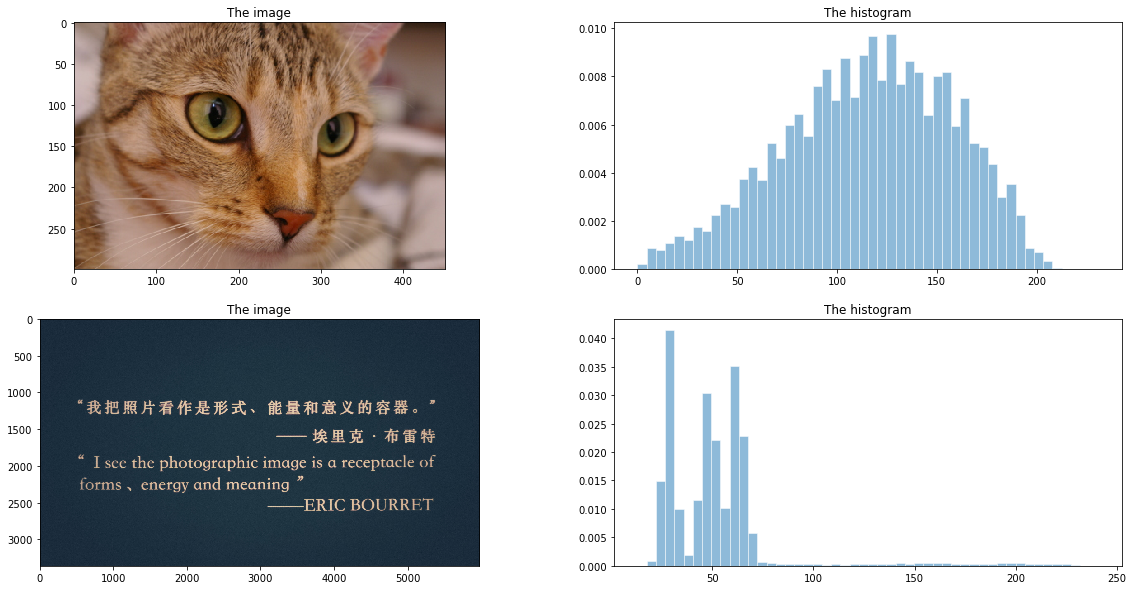
比如下图图一猫咪的直方图较为集中在中间，我们希望它的分布贴近第二幅文字图的分布（集中在暗区域）

im1
im1

数学基础

从上一篇文章的介绍中我们发现，对于任何图像（\(r\)的概率密度分布），我们都可以通过其累积分布函数将其函数变换到随机变量\(s\)，而\(s\)是均匀分布的。那我们反过来想，能否将均匀分布的随机变量逆变换到某个特定的分布呢？

公式推导

设\(r\)为随机变量值域为\([0,255]\)，其概率密度函数为\(p_r(r)\)。一函数（变换为）：

\[s = T(r) = (L-1) \int_{0}^{r} p_r(m) \mathrm{d}m\]

由上一篇文章我们易知\(s\)服从均匀分布，我们寻找一个\(z\)随机变量符合另一特殊分布\(p_z(z)\)，易知存在一函数（变换）：

\[s = G(z) = (L-1) \int_{0}^{z} p_z(m) \mathrm{d}m\]

由于\(G(z)\)为累积分布函数，单调，故存在反函数\(G^{-1}(z)\)，则有新变换 \(N = G^{-1} \cdot T\)，使得\(r\)随机变量经\(N\)变换后符合\(z\)的分布特征。

\[z = G^{-1}(s) = G^{-1}(T(r)) = N(r)\]

由此，我们找到了某值域内求从某一分布随机变量\(r\)变换到指定分布随机变量\(z\)的方法。

个人理解

直方图均衡，均匀分布，实际上在中间做了桥接。

实验效果

均衡化

输出两幅图原图以及均衡化后的图片，直方图。

im1
im1

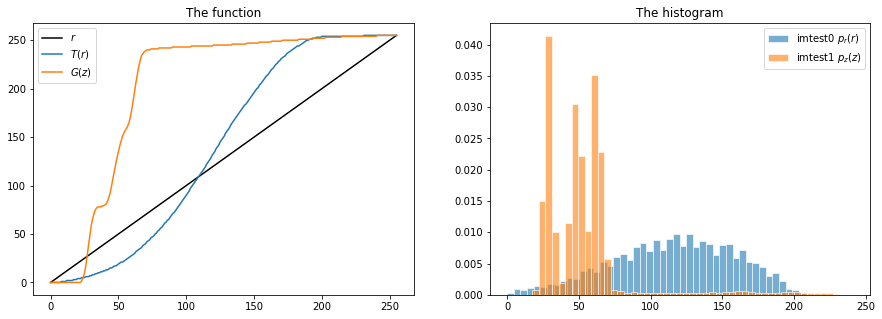
直观对比两图的累积分布函数与直方图

\(T(r)\)表示\(r\)的累积分布函数，本样例中为小猫图像的累积分布函数，图示为淡蓝色曲线。 \(G(z)\)表示为\(z\)的累积分布函数，本样例中为文字图片的累积分布函数，图示为橙黄色曲线。

im1
im1

求反函数

反函数的计算，并没有按照课本上所说，搜索找最近值，对于一张\(m \times n\)图像，对于每个搜索需要\(O(log(L))\)，总复杂度是相乘的关系\(O(MNlog(L))\)，而通过一个二重循环实现打表计算则可以优化到\(O(MN)+O(L)\)，对于实际图片\(MN\)远大于\(L\)，所以这种优化是值得的

1
2
3
4
5
6
cnt = 0
for i in range(256):
    while cnt<=raw_table[i]:
        new_table[cnt] = i
        cnt+=1
return new_table

计算反函数表方便后面对图像进行变换。

1
2
3
reverse_imtest1_table = GetReverseTable(imtest1_tabel)
match_imtest0_table = reverse_imtest1_table[imtest0_tabel]
match_imtest0 = match_imtest0_table[imtest0]

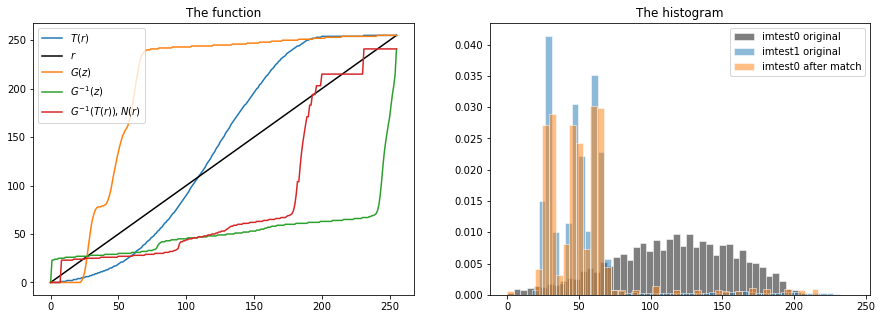
输出结果如下

im2
im2

直方图对比表示了 image0，image1，匹配后的 image0 三图，由图可以看出匹配后的 image0 直方图分布已经很贴近 image1 了。

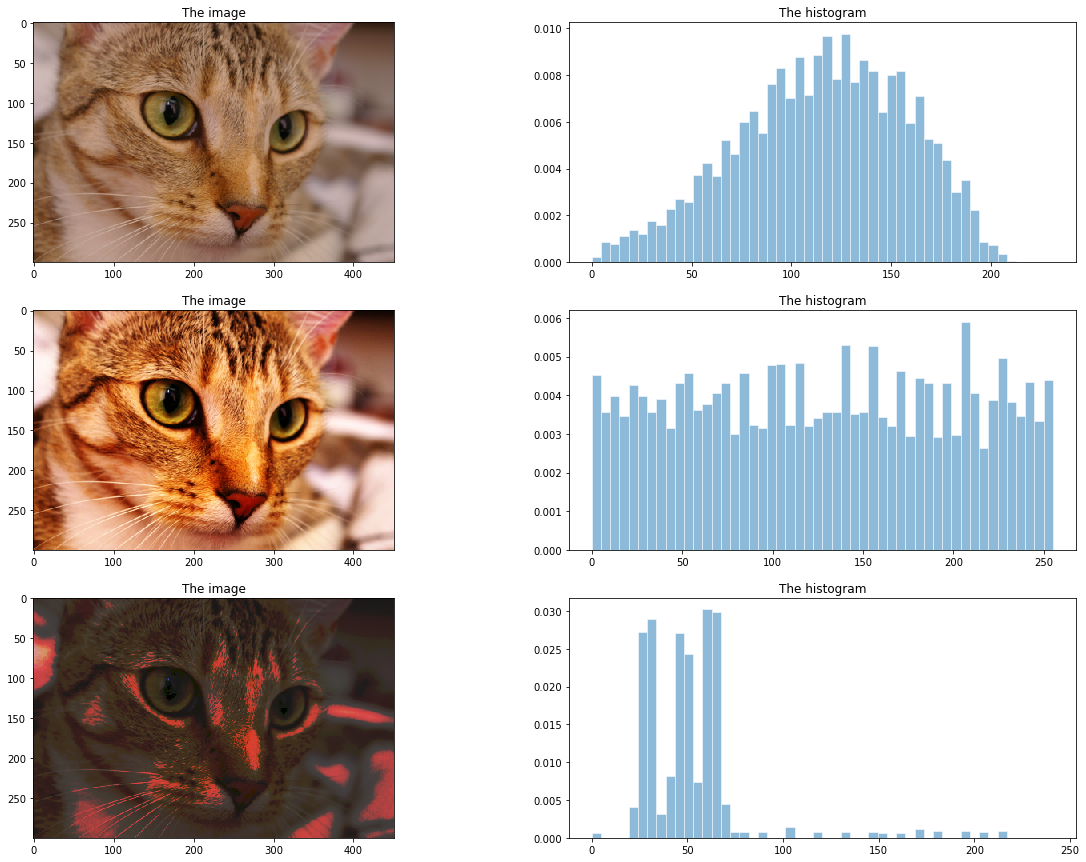
图片效果

（小猫被玩的有点可怜）

im2
im2

核心代码

图像直方图展示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 展示直方图
def DrawHist(input_img,pic_handle,histogram_handle):
    kwargs = dict(bins = 50, histtype='bar', edgecolor = "white",alpha=0.5, density  = True)
    pic_handle.set_title("The image")
    pic_handle.imshow(input_img)
    histogram_handle.set_title("The histogram")
    histogram_handle.hist(input_img.flatten(),**kwargs)

imtest0 = imageio.imread('imageio:chelsea.png')
imtest1 = GetRGB('./3_3Photo/3.jpg')

plt.figure(figsize=(20,10))
DrawHist(imtest0,plt.subplot(221),plt.subplot(222))
DrawHist(imtest1,plt.subplot(223),plt.subplot(224))

plt.show()

直方图匹配

1
2
3
4
5
6
7
8
9
10
# 获取目标图像累积分布函数的反函数lut表（离散）
def GetReverseTable(raw_table):

    new_table = np.zeros(256,dtype = np.int64)
    cnt = 0
    for i in range(256):
        while cnt<=raw_table[i]:
            new_table[cnt] = i
            cnt+=1
    return new_table

加入反函数输出

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# 加入反函数，再绘图
plt.figure(figsize=(15,5))
plotline = plt.subplot(121)
plotline.set_title("The function")
plotline.plot(np.arange(256),imtest0_tabel,label = "$T(r)$")
plotline.plot(np.arange(256),np.arange(256),color = "black",label = "$r$")
plotline.plot(np.arange(256),imtest1_tabel,label = "$G(z)$")
plotline.plot(np.arange(256),reverse_imtest1_table, label = "$G^{-1}(z)$")
plotline.plot(np.arange(256),match_imtest0_table, label= "$G^{-1}(T(r)), N(r)$")
plotline.legend()


# 设置直方图参数 分割块 叠加模式 边界颜色 透明度 正则化（映射到0~1）
kwargs = dict(bins = 50, histtype='bar', edgecolor = "white",alpha=0.5, density  = True)
histogram1 = plt.subplot(122)
histogram1.set_title("The histogram")
histogram1.hist(imtest0.flatten(),color = "black",label = "imtest0 original",**kwargs )
histogram1.hist(imtest1.flatten(),label = "imtest1 original",**kwargs)
histogram1.hist(match_imtest0.flatten(),label = "imtest0 after match",**kwargs)
histogram1.legend()

plt.show()

完整代码

1
2
3
4
5
6
import numpy as np
import imageio
import cv2
import matplotlib.pyplot as plt

im = imageio.imread('photo2.jpg')
1
2
3
4
5
6
# 获取RGB图像
def GetRGB(path):
    im_BGR = cv2.imread(path,cv2.COLOR_GRAY2RGB)
    im = cv2.cvtColor(im_BGR,cv2.COLOR_BGR2RGB)
    return im

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 展示直方图
def DrawHist(input_img,pic_handle,histogram_handle):
    kwargs = dict(bins = 50, histtype='bar', edgecolor = "white",alpha=0.5, density  = True)
    pic_handle.set_title("The image")
    pic_handle.imshow(input_img)
    histogram_handle.set_title("The histogram")
    histogram_handle.hist(input_img.flatten(),**kwargs)

imtest0 = imageio.imread('imageio:chelsea.png')
imtest1 = GetRGB('./3_3Photo/3.jpg')

plt.figure(figsize=(20,10))
DrawHist(imtest0,plt.subplot(221),plt.subplot(222))
DrawHist(imtest1,plt.subplot(223),plt.subplot(224))

plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
# 尝试直方图均衡化，
def CaculateHistogram(input_image):
    # 参数1. 单通道8位灰度图像
    # 输出1. 总像素值
    # 输出2. 灰度值分布计数
    # 输出3. 灰度值分布前缀和（用来做后续直方图平局奴化）

    # 区分通道
    if len(np.shape(input_image)) == 3:
           height,width,level = np.shape(input_image)
           summ = height*width*level
    else :
           height,width = np.shape(input_image)
           summ = height*width


#     第一种 通过访问指定位置像素  耗时executed in 7m 9s
#     巨慢无比
#     for i in range(height):
#         for j in range(width):
#             caculate_num[input_image[i][j]] += 1

#     第二种 直接拆分行，像素获取像素值  耗时executed in 14.4s
#     for line in input_image:
#         for px in line:
#             caculate_num[px] +=1

#     第三种 调用np.histogram()方法  耗时executed in 644ms
    caculate_num,index_x = GetHistogramArray(input_image)
    caculate_num = np.append(caculate_num,1)
#     print(np.shape(caculate_num))
    #     第四种 吕少推荐的方法(还没看懂)
#     caculate_num = cumsum(input_image,256)
#     print(np.shape(caculate_num))

    sum_num = np.copy(caculate_num)
    for i in range(1,256):
#         print(sum_num[i-1],caculate_num[i])
        sum_num[i] = sum_num[i-1] + sum_num[i]
    return summ,caculate_num,sum_num

def GetHistogramArray(image):
    return np.histogram(image,np.arange(0,256));

def cumsum(img, bins):

    histogram = np.zeros(bins)
    for pixel in np.arange(0, bins, 1):
        histogram[pixel] += len(img[img==pixel])

    return histogram

def HistogramEqualizationLUT(input_image):
    # 参数1, 单通道8位灰度图像
    # 输出1. 单通道8位灰度图像（直方图均衡化后）
    size,data,data_sum = CaculateHistogram(input_image)
    fxy  = lambda x: (255*data_sum[x])//size
    table = np.array([fxy(i) for i in range(256)])
#     print(table)
#     不可以这样
#     image_new = table[input_image]
    lut = lambda x: table[x]
    return lut(input_image),table


imtest0_he,imtest0_tabel = HistogramEqualizationLUT(imtest0)
imtest1_he,imtest1_tabel = HistogramEqualizationLUT(imtest1)
plt.figure(figsize=(20,20))
DrawHist(imtest0,plt.subplot(421),plt.subplot(422))
DrawHist(imtest0_he,plt.subplot(423),plt.subplot(424))
DrawHist(imtest1,plt.subplot(425),plt.subplot(426))
DrawHist(imtest1_he,plt.subplot(427),plt.subplot(428))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
plt.figure(figsize=(15,5))
plotline = plt.subplot(121)
plotline.set_title("The function")
plotline.plot(np.arange(256),np.arange(256),color = 'black',label = "$r$")
plotline.plot(np.arange(256),imtest0_tabel,label = "$T(r)$")
plotline.plot(np.arange(256),imtest1_tabel,label = "$G(z)$")
plotline.legend()

kwargs = dict(bins = 50, histtype='bar', edgecolor = "white",alpha=0.6, density  = True)
histogram = plt.subplot(122)
histogram.set_title("The histogram")
histogram.hist(imtest0.flatten(),**kwargs, label = "imtest0 $p_r(r)$" )
histogram.hist(imtest1.flatten(), **kwargs, label = "imtest1 $p_z(z)$")
histogram.legend()
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 获取目标图像累积分布函数的反函数lut表（离散）
def GetReverseTable(raw_table):

    new_table = np.zeros(256,dtype = np.int64)
    cnt = 0
    for i in range(256):
        while cnt<=raw_table[i]:
            new_table[cnt] = i
            cnt+=1
    return new_table

reverse_imtest1_table = GetReverseTable(imtest1_tabel)
match_imtest0_table = reverse_imtest1_table[imtest0_tabel]
match_imtest0 = match_imtest0_table[imtest0]


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# 加入反函数，再绘图
plt.figure(figsize=(15,5))
plotline = plt.subplot(121)
plotline.set_title("The function")
plotline.plot(np.arange(256),imtest0_tabel,label = "$T(r)$")
plotline.plot(np.arange(256),np.arange(256),color = "black",label = "$r$")
plotline.plot(np.arange(256),imtest1_tabel,label = "$G(z)$")
plotline.plot(np.arange(256),reverse_imtest1_table, label = "$G^{-1}(z)$")
plotline.plot(np.arange(256),match_imtest0_table, label= "$G^{-1}(T(r)), N(r)$")
plotline.legend()


# 设置直方图参数 分割块 叠加模式 边界颜色 透明度 正则化（映射到0~1）
kwargs = dict(bins = 50, histtype='bar', edgecolor = "white",alpha=0.5, density  = True)
histogram1 = plt.subplot(122)
histogram1.set_title("The histogram")
histogram1.hist(imtest0.flatten(),color = "black",label = "imtest0 original",**kwargs )
histogram1.hist(imtest1.flatten(),label = "imtest1 original",**kwargs)
histogram1.hist(match_imtest0.flatten(),label = "imtest0 after match",**kwargs)
histogram1.legend()

plt.show()
1
2
3
4
5
6
# 输出三种图像
plt.figure(figsize=(20,15))
DrawHist(imtest0,plt.subplot(321),plt.subplot(322))
DrawHist(imtest0_he,plt.subplot(323),plt.subplot(324))
DrawHist(match_imtest0,plt.subplot(325),plt.subplot(326))
plt.show()