Step 1

题目摘要引言

Title

针对 geo-replicated 系统的细粒度一致性（模型）

Abstract

跨地域的系统节点，提供了低延迟，但是为了保证系统整体的状态收敛以及一些不变式，跨地域的协调也是必须的。研究如何提升性能，减少高开销的跨地域同步成为研究热点。

文章提出了一个新型的一致性模型 Partial Order-Restrictions consistency(PoR consistency)。

为了提供高效的 PoR 一致的 replication，实现了 Olisipo，一个考虑受限制操作的相对频率来分配不同协调策略的协调服务（系统）。

Introduction

关于一致性的探讨，一些学者主张完全放弃强一致性而采取较弱的一致性的模型（比如 Eventual Consistency 和 Causal Consistency），其他学者则主张在单个系统中建立多层次共存的混合一致性，比如本文作者的前置工作 RedBlue Consistency，类似的混合一致性允许一部分操作在强一致性下执行，而其他操作在较弱一致性下执行。

核心是一套 labeling 的方法来帮助编程人员为不同操作赋上合适的一致性级别。方法对于一些应用是高效的，但仍然发现了一些不必要的 coordination。这里没有表述清楚，似乎是特别的一对操作间需要同步，但是不需要与其他操作同步，但是在原有机制的要求下会要求强一致性从而产生与其他操作额外的 coordination。更进一步，类似 POPL16 提出的通用的更细粒度的协调，也缺少精确的方法来识别一组限制以确保安全。

PoR，吃进一组限制，强制要求这些限制在所有偏序中满足。通过增加/减少限制来强化/弱化一致性模型。

部署应用 PoR 一致性的应用最重要的是定义一组限制条件，可以保证状态收敛并保护不变式。这是一大人工困难，作者的解决方法是设计了一些指导原则。

基本理论概况

结论部分

改进方法，结合了 conflict relation 来提供一种更加通用的方式，以冲突对的增加/减少，来对应强/弱一致性。

并且提供了一个 coordination serviced，Olisipo 来高效序列化操作。

在不同场景下运行 RUBiS 体现出新设计更高的性能。

回答基本问题

1. 类别

   对原型系统进行描述，严格的说，是参照一种 general 理论的具体系统实现。

2. 内容

   POPL16 Cause I'm Strong Enough

   OSDI12 RedBlue Consistency

3. 正确性

   待定

4. 创新点

   general, general, general

5. 清晰度

   清晰

阅读选择

继续阅读

Step 2

细读笔记

System model

"site" and "replica" are interchangeable

系统定义了操作集和可达状态集。每个操作由一个 user 在一个 site 提出，我们称之为 u's primary site，表示为\(site(u)\)。操作的数学定义是一个函数（ generator 函数 \(g_u\)），接收当前系统状态\(S\)并返回一个函数与 side effects 相对应的函数（shadow 函数，\(h_u(S)\)）。（这里已经十分贴近 POPL16 中的数学描述了

从实现角度来说，generator 函数会现在 primary site 的沙盒中进行，不与其他并发操作交互，之后会将其 side effect 对应的 shadow function 传递给其他 replica 并执行。

一条预定的性质：任意 replica 执行了相同 shadow operation 集后达到相同的状态，收敛性要求。（回忆 POPL 的交换性）。另外系统还需要维护一组特定于应用程序的不变式。

RedBlue consistency

RedBlue consistency，将 shadow operations 分离为 blue operations :blue_circle: 和 red operations :red_circle:

• blue operations :blue_circle: :执行顺序在不同 site 中可以是不同的。
• red operations :red_circle: :在所有 site 中都要保持相同的相对顺序。

为确保收敛，red operation 的一个充分条件，如果它不是全局通信的。为确保不变式，（这里有些没太听明白），被作用在与 generate 不同的状态的所有阴影操作都要标红？pass checks 的标蓝。

Partial Order-Restrictions consistency

Motivation

eBay-like auction service

RedBlue 的解决方法，既然\(\mathsf{placeBid}\)操作和\(\mathsf{closeAuction}\)和本应用特定的 invariant 产生冲突，就应该全部标注为 red。

而这种情况下，label 这两个操作在这个简单的应用中等同于将一致性强化为强一致性。任意两两操作之间的执行顺序都是确定的，正如同自己所想，实际上\(\mathsf{placeBid}\)的操作是不需要 order 的，因为 order 不影响最后的 winner 人选。

交给 PoR，允许 developer 在单一系统中推理各种细粒度一致性。

关于状态收敛与保证不变式

A Glimpse of Olisipo

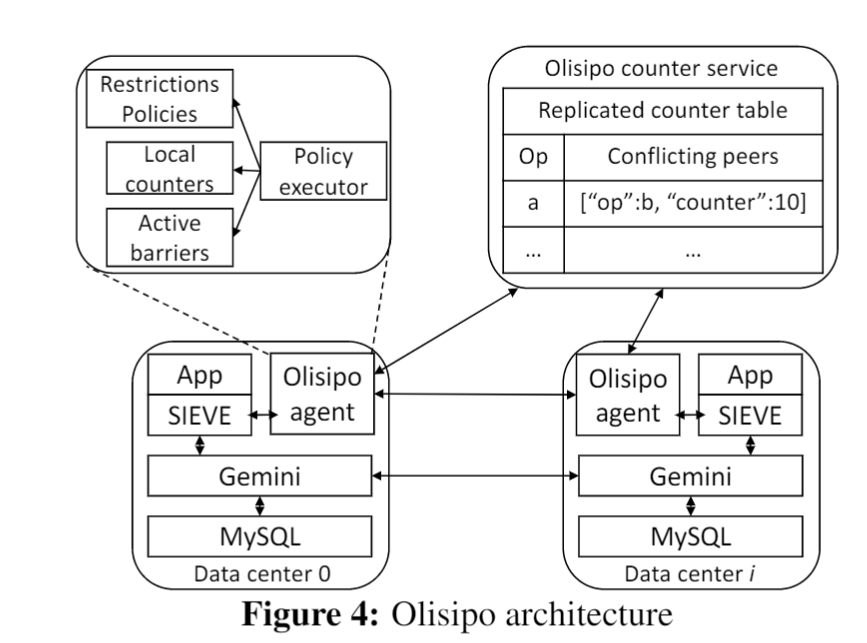
一般来说？通过 Paxos 和 Raft 实现的一致性系统满足强一致性。根据先前对 \(\mathsf{placeBid}\)操作和\(\mathsf{closeAuction}\)操作的分析，设计一个 coordination service，命名为 Olisipo，来提供各种 coordination 策略。Trade-off: cost of each op and the overall cost. 记录了运行时的操作的执行平吕来选择更高效的 coordination 机制。

Coordination protocols

two built-in protocols, symmetric(Sym) and asymmetric(Asym)，支持拓展更多定制的 coordination 策略（需要根据文章要求配置指定的接口）。主要区别：

• symmetric：the restricted op \(u\) and \(v\) coordinate with each

• asymmetric：one as default and the other to obtain permission

• Sym.:

  维护一个中心的逻辑计时服务。对于每一对限制\(r(u,v)\)，两个 counters \(c_u\)和\(c_v\)。每一个都代表相对类型操作被底层系统接受的总数。每个 replica 保留一份 counters 的 copy，用以记录被该 replica 执行的操作的数量。

  初始，所有 replica 的本地 counter 和全局 counter 都初始化为 0。当一个 replica 接收到操作时，先使本地 counter 服务联络全局 counter 增加相关操作类型的计数器，然后返回一个最新的计数器副本。比对，如果相同（表示没有并发其他操作？）则立即执行，否则除非其他缺失操作（递交到其他 replica 还没有传递到本地）被本地 relica 接收到。

  counter-service 的容错性由一个 Paxos-like 的状态机复制模型提供。

• Asym.：

  去中心方式来实现分布式限制（障碍 barrier）。当一个受限制操作对\((u,v)\)中的\(u\)陷入某一个 replica 的 barrier 中，会向其他 replica 广播加入申请。这要求其他 replica 都停止\(v\)的操作，直到接收所有 replica 的许可后，\(u\)才会被执行，并通知所有的 replica 自己已经离开 barrier（在本通知中也附带刚刚执行的\(u\)的影响）。

  执行负担很大，如果操作中的一边较少出现会有改善（问题，仍然要陷入 barrier 和接受 ACK，为什么会改善？）

  

  PoR_01.png

问题记录

未读（且值得读）文献记录

Step 3

思路复现

Partial Order-Restrictions consistency

Defining PoR consistency

1. a set of Restrictions
2. a restricted partial order(R-order)
3. a set of site-specific causal serializations

Def 1 (Restriction). Given a set of operations \(U\), a restriction is a symmetric binary relation on \(U \times U\)

For any two operations \(u\) and \(v\) in \(U\), if there exists a restriction relation between them, we donate the relation as \(r(u,v)\).

Def 2 (Restricted partial order). Given a set of operations \(U\), and a set of restrictions \(R\) over \(U\), a restricted partial order (or short, R-order) is a partial order \(O = (U,\prec)\) with the following constraint

\[\forall u,v \in U, r(u,v) \in R \Rightarrow u \prec v \lor v \prec u\]

注意这里或的关系，Restricted 关系导出的 R-order 是取对称的一边。

This definition places constraints on a global view of a replicated system;

证明与推理复现

实验验证复现