数据分析与融合——偏序格角度看决策系统代数约简

偏序格角度看决策系统代数约简

基本知识：

  • 一个集合的所有划分构成一个细分偏序格。
  • 决策系统约简始终保持决策系统的一致性（不存在条件相同，决策不同）。
  • 对于一个决策系统来说，约简是条件分类\(U/C → U/A\)的过程，而条件分类\(U/C\)细分\(U/A\)。

引发思考：

课程的结尾老师提到我们的决策系统约见过程，其条件分类可以看作是在一个论语元素的全部划分构成的细分偏序格上寻优的过程。

直观上给人的感觉是这样的，这篇文章主要是想回过头来，从偏序格角度回看这一寻优过程，并解决以下疑惑：

  • Q1.为什么可以看做是细分偏序格上的寻优？
  • Q2.寻优的终点（极小值）对应的是哪个（些）结点，有没有什么特征？
  • Q3.寻优的路径是怎样的，有没有什么特征，是否会与“偏序”产生关系？

带着这些疑问，我开始了自己的琢磨。

由于里面一些很数学的东西并没有细致详尽的证明，我只能从数学角度看待，还不算科学的证明，有待于后面复习时巩固数学部分的证明。

Q1.寻优的解释

为方便描述，我们使用老师所给出的决策系统样例。

png
png

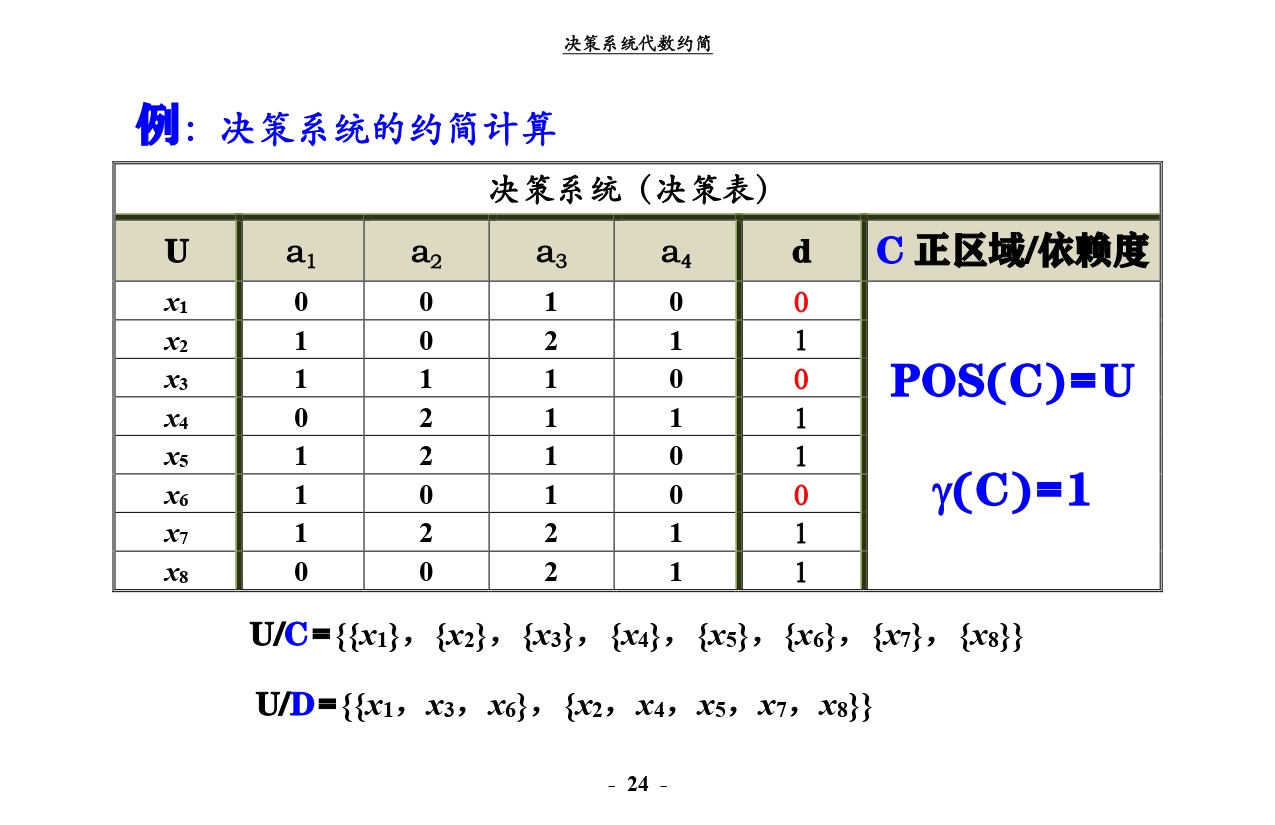
同时做以下约定，与一些教材（包括老师提供的讲稿）中有些许不同：

  • \(U\)为论域元素集合
  • \(Road_1,Road_2 \cdots\) 表示约简路径 1，2 等等。
  • \(C\)为最初的属性集合，为方便约见过程中属性集的变换，我们再做以下规定。
    • \(C_{i1}\)表示约简路径\(Road_i\)上的第\(1\)次约简后的属性集，及初始状态，所以易知，\(C_{i0} = C\)
    • \(C_{ij},j \not ={0}\)表示约简路径\(i\)上的第\(j\)次约简后的属性集。
  • \(D\)为决策值集合

约定都完成了，我们该如何解释“约简”可以看做是细分偏序格上的寻优过程呢？我想可以从细分偏序格上结点，和路径两点与我们约简不同阶段的状态和转移过程对应起来

结点 and 状态

细分偏序格图示上每个结点对应一个划分，而我们决策系统约简过程中，每一个约简前后的状态实际上也是一个论域的划分。

举例 1，根结点，未分类状态。

此时也未进行决策系统一致性检测，这么说的原因是，我们还未用\(C_{i1}\)进行任何一次属性集上的等价类划分，此时每个元素都是相互分开的，

png
png

举例 2，初始决策系统检测结点，由于我们这个表中没有重复项，所以应用\(C_{i1} = C\)（对于任意一条路径都一样，所以用了\(i\)表示），得到的划分仍然是原来的划分（对于带重复项的则不然）。

png
png

举例 3，\(C_{01} = C_{00}- a_1\)，约简\(a_1\)后，划分\(U/C_{11} = \{ \{ x_1, x_6 \} , \{ x_2, x_8 \} , \{ x_3 \} , \{ x_4 \} ,\{ x_5 \} , \{ x_7 \} \}\)。

jpg
jpg

其对应的结点为

png
png

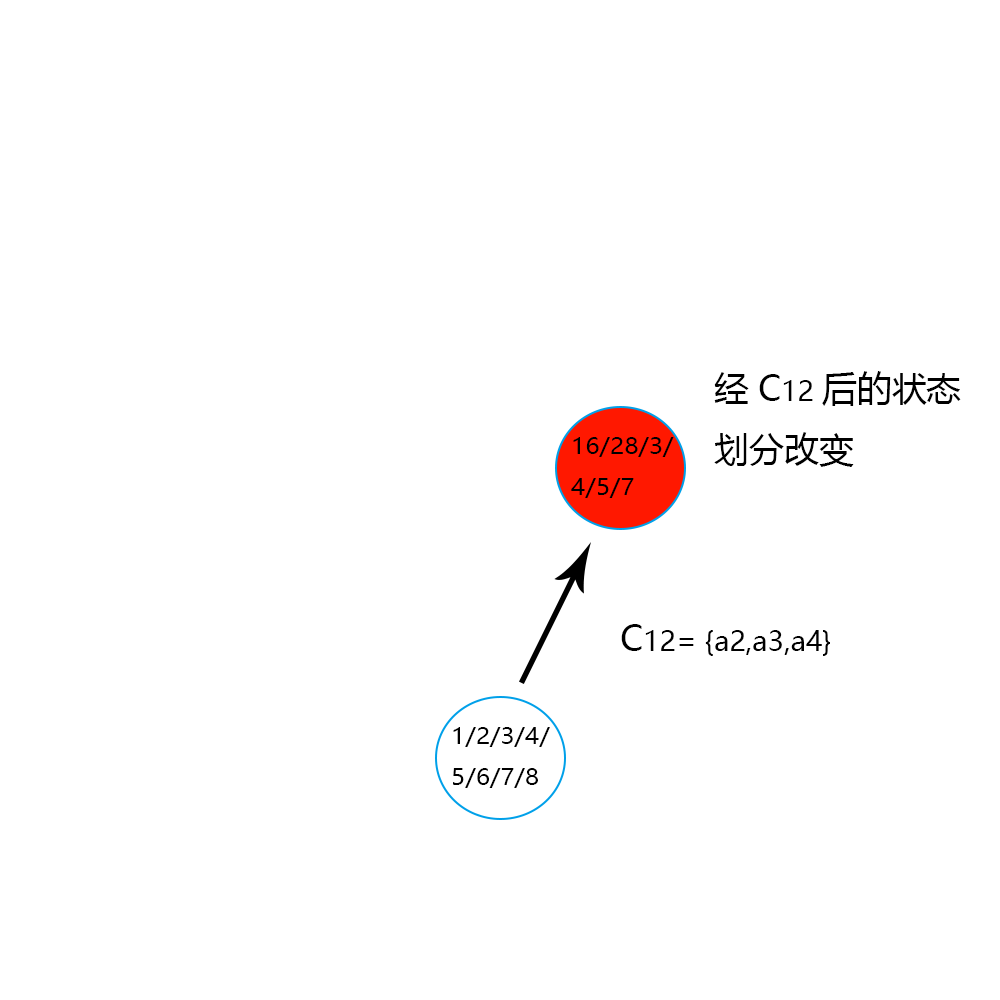
路径 and 转移过程

在最前面的基本知识已经提到了：

对于一个决策系统来说，约简是条件分类\(U/C → U/A\)的过程，而条件分类\(U/C\)细分\(U/A\)。

换言之，我们一条路径上约简的结点状态变化应该为\(U/C_{i1} \rightarrow U/C_{i2} \rightarrow U/C_{i3} \cdots\)，而前者都是细分后者的，所以必然是细分偏序格向上的方向。

一点数学解释：由于是约简，我们可以确定一条路径上 \(C_{ij}\subseteq C_{ik}\)对任意\(j<k\)，故其确定的等价关系 \(R_{ij} \subseteq C_{ik}\)，而由商集的性质易知其细分关系。

举例，如约简两次达到最终的不可约简状态，转移图。

png
png

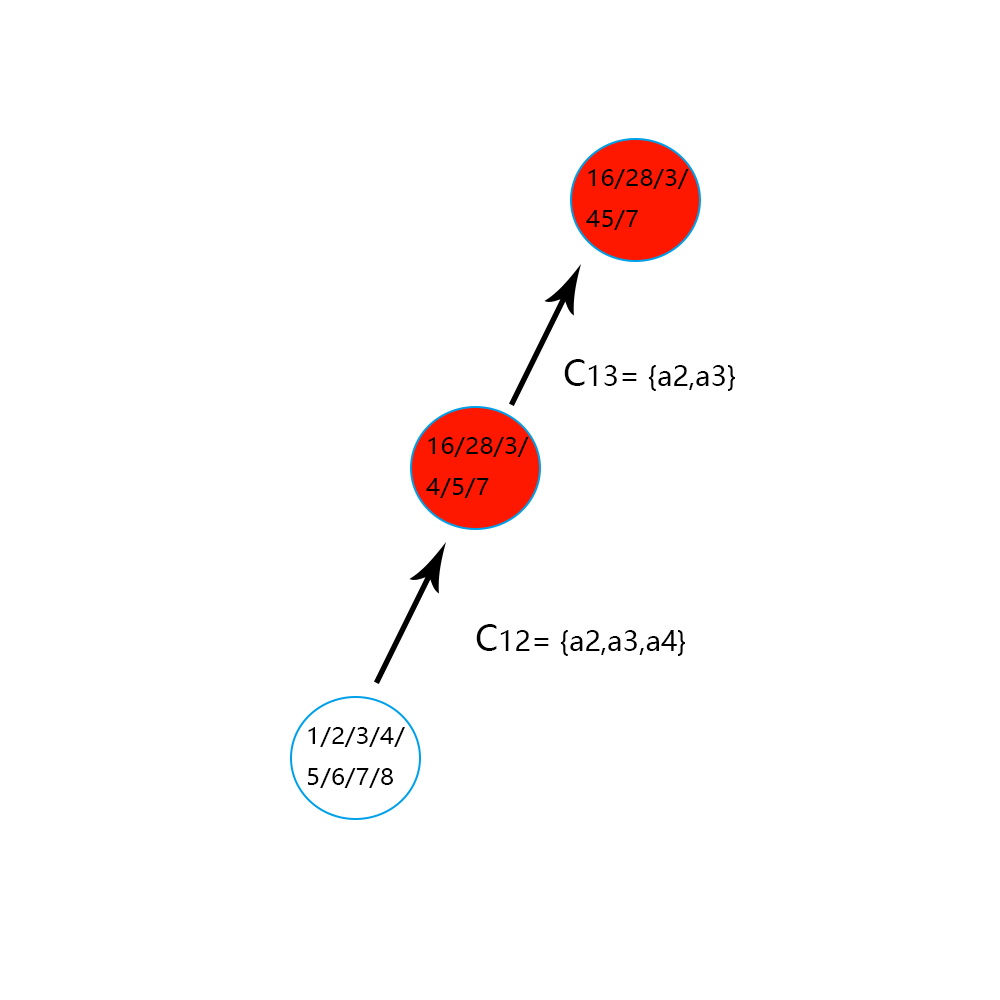
需要提起注意的是，箭头并非只代表细分偏序格 Hasse 图中的那些边，而是代表 precede，可能是多条 Hasse 图中边（即跨越了一些状态），这也是我后面探索的问题的来源。

Q2.最终状态点与极小属性集

在课上我也问到了老师这样一个问题，我们找到的约见后条件属性集是“极小”而非最小，因而有可能会存在多个。

jpg
jpg

而这个样例中确实存在两个“极小”。分别应该是：

  • \(C_{13} = \{a_2,a_3 \}\) 即刚刚演示的路径和最终状态
  • \(C_{23} = \{a_2,a_4 \}\)

进一步观察，他们对应细分偏序格上的状态是不同的（路径也是不同的），也即\(U/C_{13} \not ={ U/C_{23}}\)，相同特征是，他们必位于他们各自寻优路径

他们对应的划分如下：

\[U/C_{13} = \{ \{ x_1, x_6 \} , \{ x_2, x_8 \} , \{ x_3 \} , \{ x_4 ,x_5 \} , \{ x_7 \} \}\]

\[U/C_{23} = \{ \{ x_1, x_6 \} , \{ x_2, x_8 \} , \{ x_3 \} , \{ x_4 ,x_7 \} , \{ x_5 \} \}\]

路径图示如下：

png
png

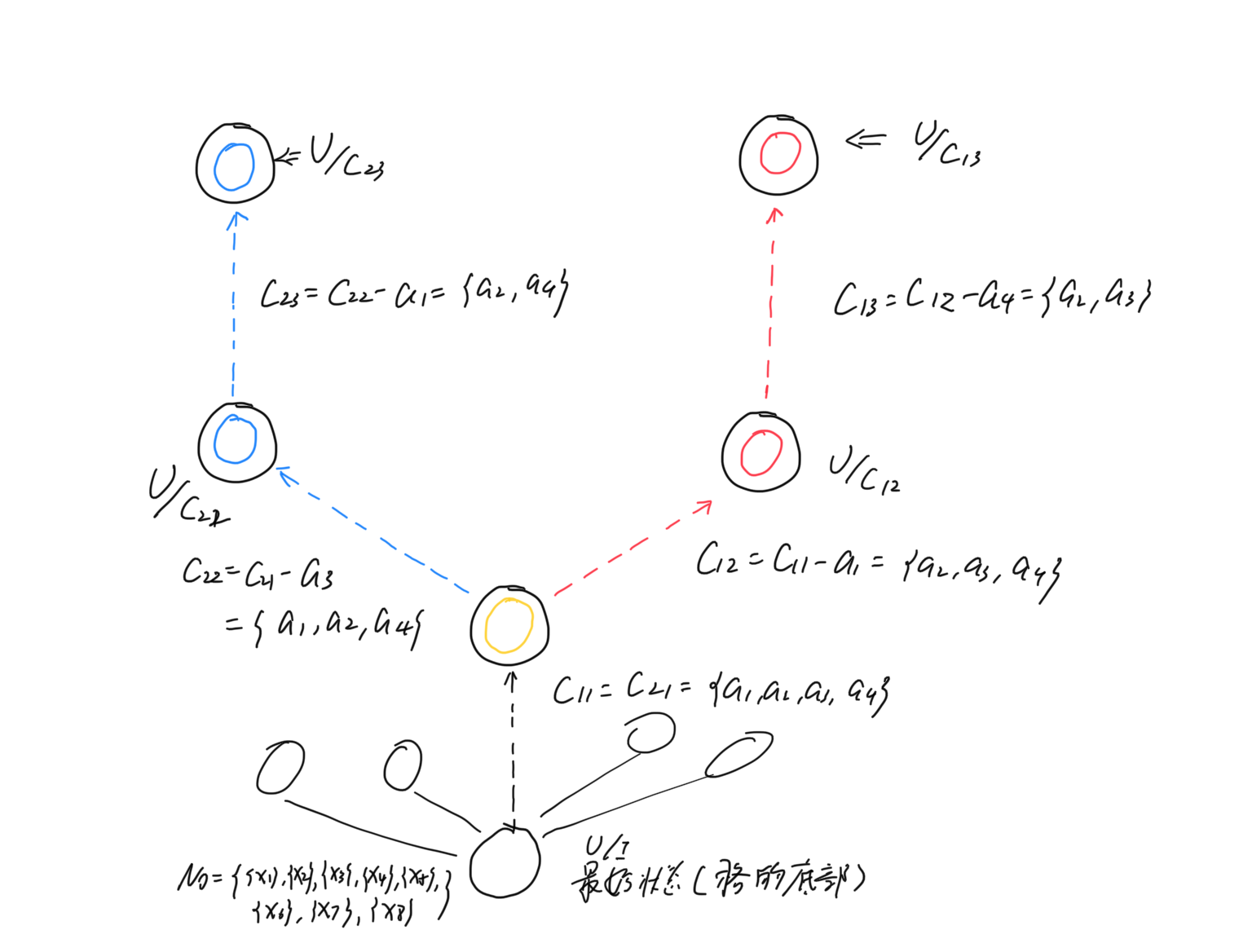
发现改变在\(x_4,x_5,x_7\)上，试图寻找一些关联性。我回去复查了以下原始的表。

png
png

发现在决策列\(x_4,x_5,x_7\)均为\(1\)，这其中有什么相关性吗？联想上图下面给出的决策划分：

\[U/D = \{ \{ x_1, x_3 ,x_6 \} , \{ x_2, x_4,x_G5 ,x_7, x_8 \} \}\]

同时联想到我们约简过程，相对正域，始终都必须要满足我们的条件划分元素\(X_i\)被决策划分的元素\(Y_j\)包含，所以我们的约简过程最初就存在一个上界，就是\(U/D\)，图示如下。

png
png

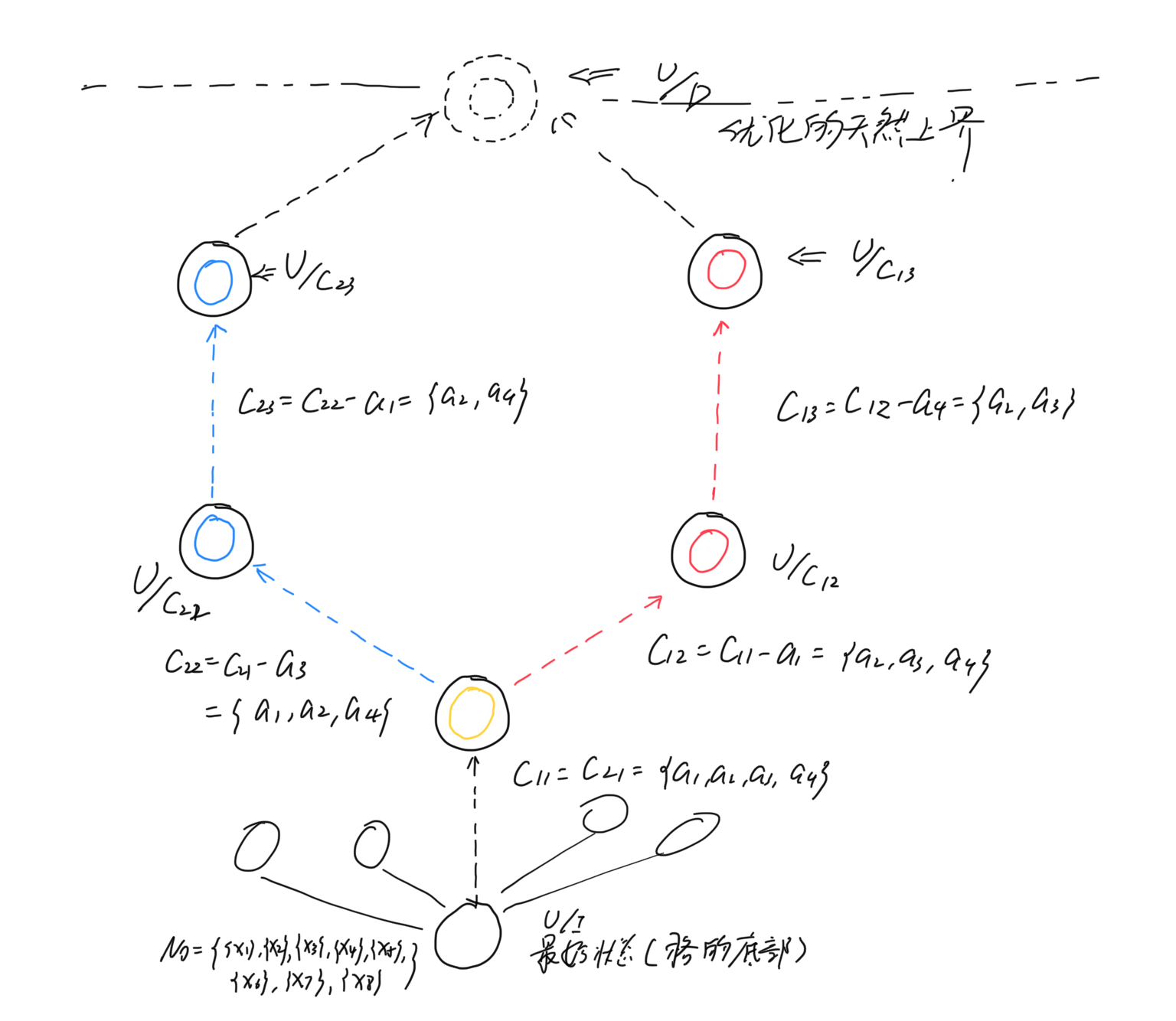
还是数学上的解释，唯有当我们的划分\(U/C = U/D\)即条件划分与决策划分相等时，这时就存在寻优后的“最小”集了，而且是唯一的，除此之外，都有可能出现多条路径多种划分方式，而且不同路径上的划分状态一般是不可比的（除非是“分叉”路径，后面会举例），如下面\(U/C_{23}\)和\(U/C_{12}\)就不具备可比性。

还有一些其他性质，比如我们发现的\(x_4,x_5,x_7\)决策值相等，我们实际上时可以证明的。当两个极小划分满足下列情况时有相关结论：

  • 划分\(U/C_p\)有如下元素\(\{ x_i,x_k , \cdots \}\)
  • 划分\(U/C_q\)有如下元素\(\{ x_i,x_l , \cdots \}\)
  • 则可证\(x_i[d] = x_k[d] = x_l[d]\) ，其中\([d]\)表示元素对应的决策值。

证明：可用上述上界证明，由于\(U/D\)的存在，而\(U/C_p \le U/D\)，\(U/C_q \le U/D\)，则\(U/D\)中必存在一集合\(A\)，满足\(x_i,x_k,x_l \in A\)，因而三者的决策值相等。

Q3 寻优路径相关

根据前述，我已经解释过，我们一次约简并不对应 Hasse图中的一条短边，而可能是多条边的集合，上面的手绘图已经给出了，从根节点到原属性划分时的跳跃情况。

这里，我关心的心问题是，对于\(Road_1\)来说，由偏序关系，当我确定我一条路径的最终状态\(U/C_{13}\)，这个划分后，易知其必定被其他\(U/C_p\)细分，\(C_p\)满足\(C_p \subseteq C_{13},C_{13} = \{a_2,a_3\}\) ，而与我去掉属性的先后顺序无关，简言之，对于我们实验的这个表，实际上还有很多路径，现在尝试手绘描述以下。

png
png

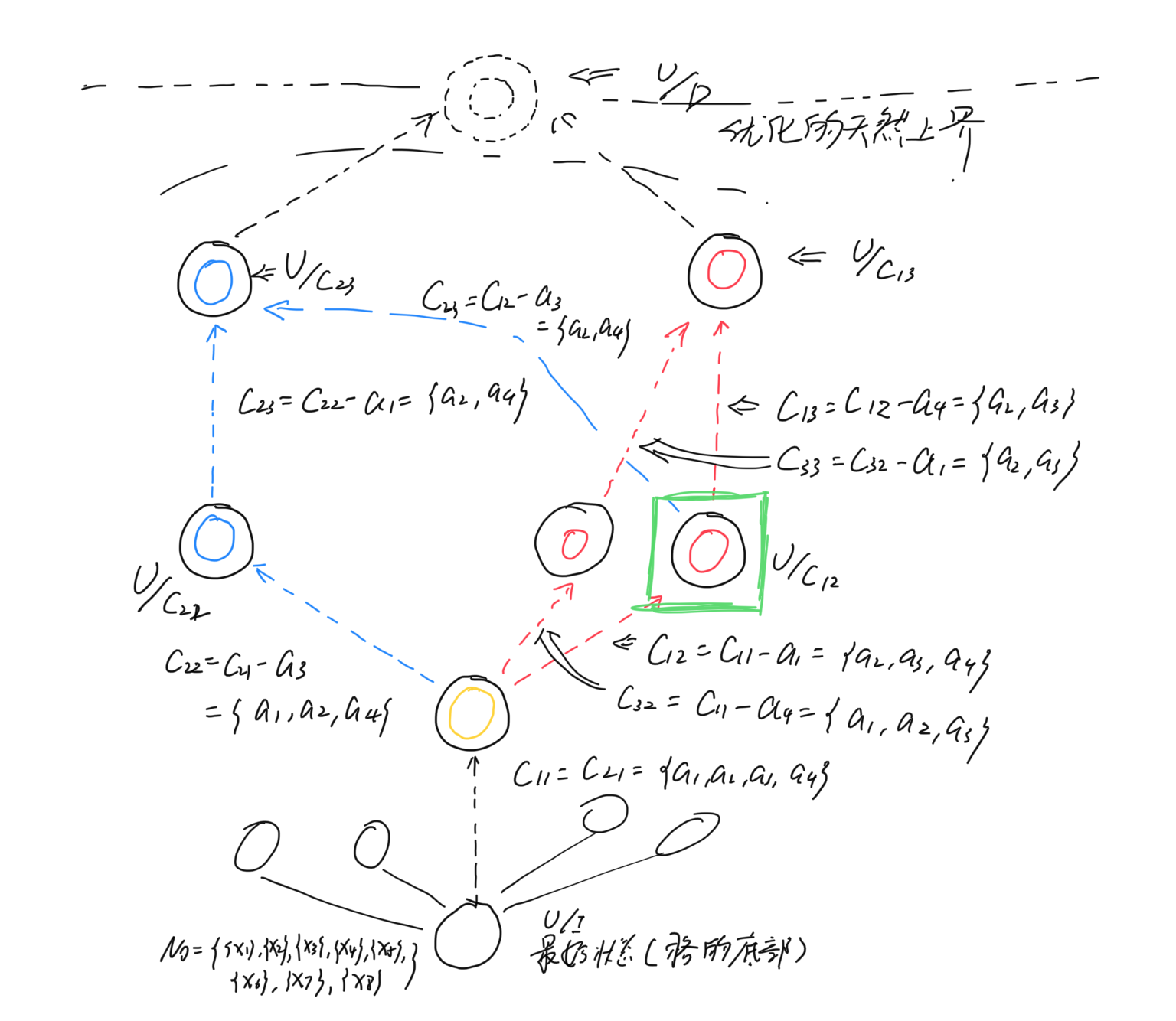
绿色框特殊标注，因其在后面可以产生到两个极小的状态。

这也实验直观感受了，即便我们的寻优是多条 Hasse 图边的组合，其路径依然在最终状态确定后反推时具备多样性。