建议阅读

《SHA-3 标准 Keccak 算法的安全性分析与实现》西电硕士论文

现代密码学：Hash 函数 Keccak

Hash 函数安全性

通常，在讨论 Hash 函数安全性时，我们常考虑下面三条性质，由于各种资料叫法不尽相同，这里做个总结。

Collision Resistacne 扛碰撞性

It should be difficult to find a pair of different messages \(m_1\) and \(m_2\) such that \(H(m_1) = H(m_2)\)

又称为强扛碰撞性（Strong Collision Resistance），指已知 Hash 算法，找出两个原像（消息、数据报文）\(m_1,m_2\)，使得其映像（消息摘要、数据摘要）\(H(m_1) = H(m_2)\)是困难的（计算不可行）。

Preimage Resistance 扛原像攻击

Given an arbitrary n-bit value \(y\), it should be difficult to find any message \(m\) such that \(H(m) = y\)

描述了数学中函数的不可逆性，扛原像攻击也称单向性（One-way）。指已知 \(y = H(m) , y \in Y\)（消息摘要，或者称数据摘要集合），要找出 \(m \in M\)（数据报文集合），使得 \(H(m)=y\) 是困难的。

Second Preimage Resistance 抗第二原像攻击

Given message \(m_1\), it should be difficult to find any different message \(m_2\) such that \(H(m_1) = H(m_2)\)。

与 Collision Resistance 很相似，就差在一个确定的原像，所以该性质又被称为弱扛碰撞性（Weak Collision Resistance）。已知 \(m_1 \in N\)， 找出另一个 \(m_2 \in M\)，使得 \(H(m_1)=H(m_2)\)是困难的（计算不可行）。

生日攻击

与 Hash 安全性放在一起介绍的生日悖论与生日攻击请自行查阅资料理解。

Keccak-f 理解

读完赛题可以确定的 Keccak 版本是(b=1600,r=1088,c=512)，也即 SHA3-256（Federal Information Processing Standards），见 Meicheng Liu 那份 PPT 第 7 页表格。

至于 b,r,c 对应海绵结构示意图位置，我在 ppt 上画了个草稿。

Keccak

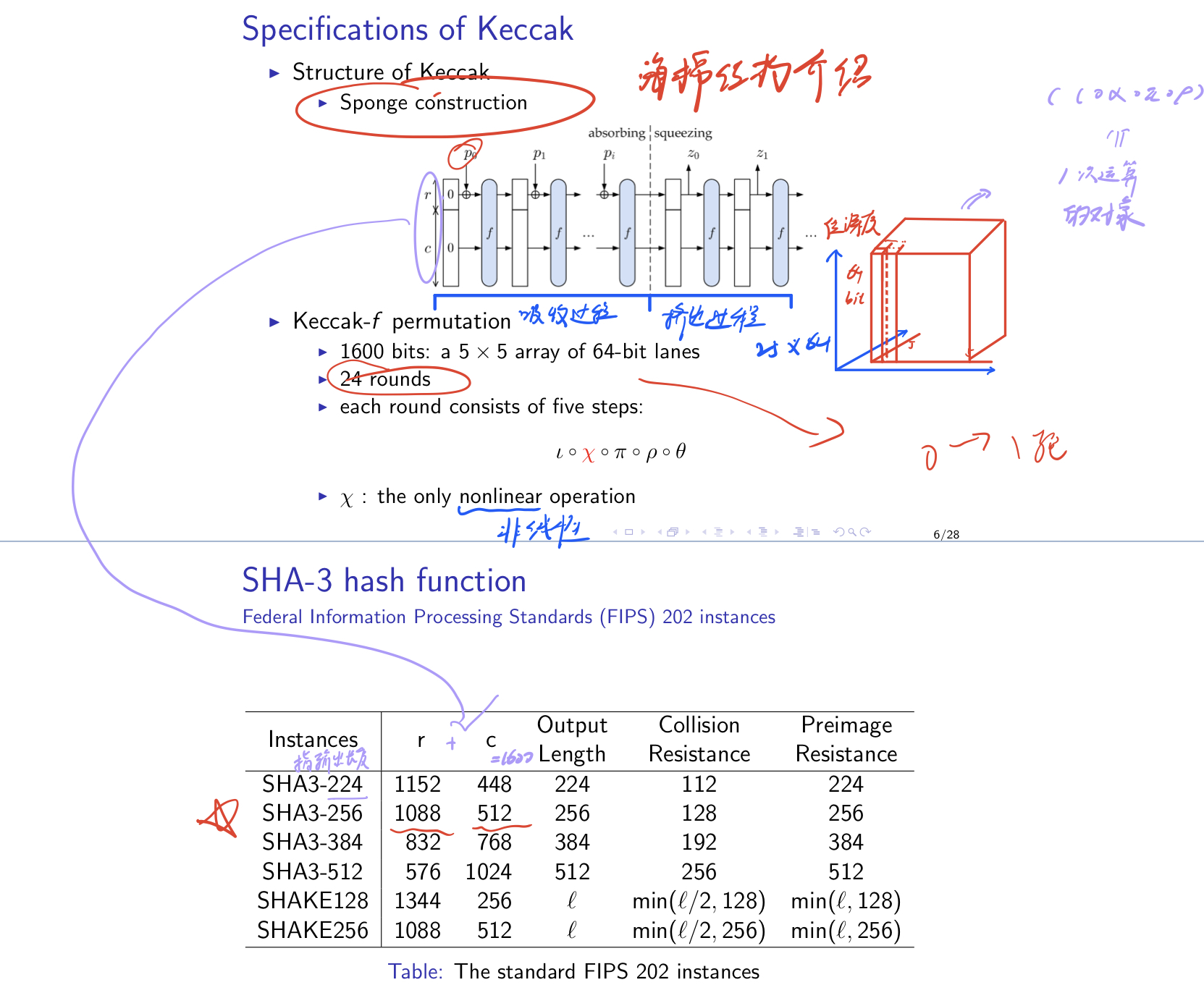
如果觉得太乱，我文字简单解释一下。

• \(b\)是总运算码长，称为置换宽度，也就是海绵体结构总长度，这个长度被拆成两个部分：\(b=r+c\)，
• \(r\)比特率（bit rate），与消息块长度相等
• \(c\)容量（capacity），表示容量（或者叫冗余长度？）
• 这两部分的区别，在每一次\(f\)置换函数轮转前，需要与原消息进行异或，但是不是整个长度\(b\)去和消息异或，只有\(r\)长度部分异或，而\(c\)部分则直接使用上一次置换计算后的结果。（这是各种利用海绵结构进行 Hash 算法的公共特征）。所以你再去看赛题第二页下方，内层第一个 for 循环只计算了\((s_0,s_1,\cdots,s_{1087})\)，长度为\(r=1088\)。而内层第二个 for 循环则表示\(f\)（置换函数）的过程，计算\((s_0,s_1,\cdots,s_{1599})\)。\((s_{1088},\cdots,s_{1599}\)这个长度为\(c=512\)部分，沿用上一次\(f'\)置换函数计算后的结果。
• 可能你会问怎么保证原消息一定是 1088 啊，当然不是。
• 我们通过补位原始至长度为 1088 的整数倍，\(k= \frac{size}{r=1088}\)，这样就解释了赛题种外层循环和\(k\)的含义，海绵结构 absorb 过程就是我们把原消息拆分成每 1088 长度为一段，逐段压入过程，压入就是前面说的两个内层循环（1088 长度异或+n 轮置换）
• Keccak-f 算法轮数\(n\)并不是指最外层 absorb-squeeze 这个过程的次数，实际上，它表示一次$
• f$（置换函数）使用 5 种运算子整体混淆的次数。这个在上面提到过了，再强调一遍。

混淆运算子

这是我自己起的名字，那几个符号不太好打我就截图了。各种 Keccak 算法介绍的资料中描述了这五个运算的实质。

Keccak

Keccak

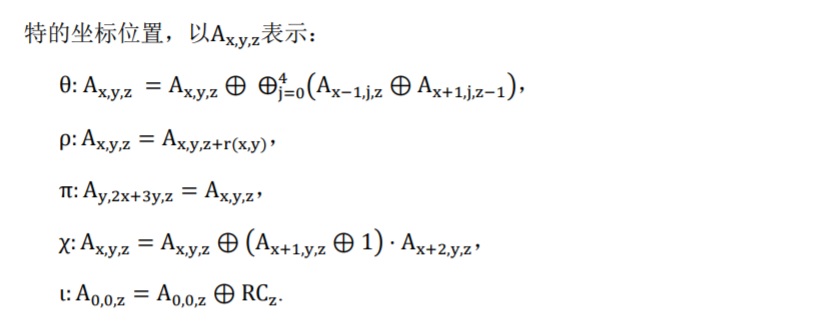
• 把\(1600\)一维长度理解成\(5*5*64\)三维 cube 有助于理解这几个运算子
• 上面两个图的描述是完全等价的，\(\theta\)虽然看起来感觉不太像，你们可以自己证一下（下次问）。
• 倒数第二个运算子根据材料讲是唯一的非线性运算子，这里我不大明白，也没想出来它的运算方式，需要你们帮我理解一下。
• RC 值与轮数有关，RC 在 24 轮中的定义如下：（这个也是个常用手段，可以先不理解 RC 值怎么来的）

const uint64_t RC[nr] = {
    0x0000000000000001, 0x0000000000008082,0x800000000000808A, 0x8000000080008000,
    0x000000000000808B, 0x0000000080000001,0x8000000080008081, 0x8000000000008009,
    0x000000000000008A, 0x0000000000000088,0x0000000080008009, 0x000000008000000A,
    0x000000008000808B, 0x800000000000008B,0x8000000000008089, 0x8000000000008003,
    0x8000000000008002, 0x8000000000000080,0x000000000000800A, 0x800000008000000A,
    0x8000000080008081, 0x8000000000008080,0x0000000080000001, 0x8000000080008008};