原始题目
小希的迷宫
- Time Limit: 2000/1000 MS (Java/Others)
- Memory Limit: 65536/32768 K (Java/Others)
- Total Submission(s): 67235
- Accepted Submission(s): 21092
Problem Description
上次Gardon的迷宫城堡小希玩了很久(见Problem B),现在她也想设计一个迷宫让Gardon来走。但是她设计迷宫的思路不一样,首先她认为所有的通道都应该是双向连通的,就是说如果有一个通道连通了房间A和B,那么既可以通过它从房间A走到房间B,也可以通过它从房间B走到房间A,为了提高难度,小希希望任意两个房间有且仅有一条路径可以相通(除非走了回头路)。小希现在把她的设计图给你,让你帮忙判断她的设计图是否符合她的设计思路。比如下面的例子,前两个是符合条件的,但是最后一个却有两种方法从5到达8。
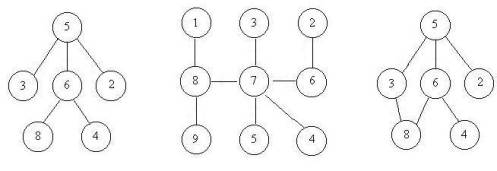 1.jpg
1.jpg
输入包含多组数据,每组数据是一个以0 0结尾的整数对列表,表示了一条通道连接的两个房间的编号。房间的编号至少为1,且不超过100000。每两组数据之间有一个空行。 整个文件以两个-1结尾。
Output
对于输入的每一组数据,输出仅包括一行。如果该迷宫符合小希的思路,那么输出"Yes",否则输出"No"。
6 8 5 3 5 2 6 4
5 6 0 0
8 1 7 3 6 2 8 9 7 5
7 4 7 8 7 6 0 0
3 8 6 8 6 4
5 3 5 6 5 2 0 0
-1 -1
Sample Output
Yes
Yes
No
Author
Gardon
Source
HDU 2006-4 Programming Contest
Recommend
lxj
题目大意
如题
解题思路
判定条件:
- 是否为一棵树,即两点之间是否只有一条途径。
- 是否包含全部点(即并查集森林大小为1)
条件1判断:用标准并查集对于每次合并检查是否已在一个集合中,若在,说明已有路径,则不满足题意。
条件2判断:set储存出现的点,\(fa[x]==x\)来判断是否为根节点。
解题代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
| #include <cstdio>
#include <cstring>
#include <iostream>
#include <set>
#include <queue>
#include <vector>
#include <stack>
#include <vector>
#include <algorithm>
#include <string>
#include <iostream>
#include <iomanip>
#include <map>
#include <unordered_map>
using namespace std;
const int maxn=1e5+5;
const int maxm=1e5+5;
typedef long long ll;
typedef unsigned long long ull;
typedef vector<int> vi;
typedef pair<int,int> pii;
typedef pair<string,string> pss;
#define rep(i,a,n) for(int i=a;i<n;++i)
#define per(i,a,n) for(int i=n-1;i>=a;--i)
#define cl(x,a) memset(x,a,sizeof(x))
#define pb push_back
#define np next_permutation
#define mp make_pair
#define INF 0x3f3f3f3f
#define EPS 1e-8
int fa[maxn],cnt[maxn];
set <int> s;
int n,m,k,t;
void init(){
rep(i,0,maxn){
fa[i]=i;
cnt[i]=1;
}
s.clear();
}
int find(int x){
if(fa[x]==x) return x;
else {
fa[x]=find(fa[x]);
return fa[x];
}
}
bool merge(int x,int y){
int fx=find(x),fy=find(y);
if(fx==fy) return false;
else {
fa[fy]=fx;
cnt[fx]+=cnt[fy];
return true;
}
}
int check(int x){
return cnt[find(x)];
}
int u,v;
int main(){
ios::sync_with_stdio(false);
init();
bool flag= true;
while(cin>>u>>v && u!=-1 && v!=-1){
if(!u && !v){
if(flag){
if(s.empty()) cout<<"Yes"<<endl;
else{
set <int>::iterator it;
int ccnt=0;
for(it=s.begin();it!=s.end();it++){
if(fa[*it]==*it) ccnt++;
}
if(ccnt==1) cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
}
else cout<<"No"<<endl;
init();
flag = true;
}
else {
s.insert(u);s.insert(v);
if(merge(u,v)==false) flag=false;
}
}
}
|
收获与反思
