引言

在前述的课程中，我们学习了粗糙集理论以及其应用：决策系统代数约简。在上一篇相关文章《数据分析与融合——偏序格角度看决策系统代数约简》，我也总结了课程的相关内容，其中，有一个明显而又重要的结论：决策系统的约简实际上是在论域元素\(U\)的细分偏序格上的寻优过程。

随着课程深入，我们又接连学习了分辨矩阵、证据理论、证据计算等，在学习证据计算这一章节时，由证据理论，我们引入了证据空间，基元等概念，从知识粒度的角度思考，其理论框架和前述学习的粗糙集及其所应用的决策系统约简有一定的相似性。

本文主要从一个基本问题——有限集合的幂集上的包含关系是否构成格，来研究粗糙集与证据理论这两套框架的相似性。

离散数学基础

集合、关系：

按照离散数学中学习的定义（虽然我不大清楚所学是朴素集合论还是康托尔公理化集合论）。
偏序关系：

\(R\)是集合\(S\)上的一个二元关系，且\(R\)满足：自反性、反对称性、传递性，则\(R\)为集合\(S\)上的偏序关系，记作\(\preceq\)
偏序集：

若在集合\(S\)上给定一个偏序关系\(\preceq\)，则称集合\(S\)按偏序关系 \(\preceq\) 构成一个偏序集合，集合 \(S\) 和偏序 \(\preceq\) 一起称为偏序集，记作\((S,\preceq)\)
哈塞图：

解释略
极大元素与极小元素：
- \(a\)在偏序集\((S,\preceq)\)中是极大的，当不存在\(b \in S\)使得\(a \preceq b\)
- \(a\)在偏序集\((S,\preceq)\)中是极小的，当不存在\(b \in S\)使得\(b \preceq a\)
上界与下界：
- \(\exists u \in S\)使得\(\forall a \in A, a \preceq u\)，即\(u\)偏序大于偏序集\((S, \preceq)\)的子集\(A\)中所有元素。那么\(u\)叫做\(A\)的一个上界。
- \(\exists l \in S\)使得\(\forall a \in A, l \preceq a\)，即\(l\)偏序小于偏序集\((S, \preceq)\)的子集\(A\)中所有元素。那么\(l\)叫做\(A\)的一个下界。
- 若\(S\)的子集\(A\)存在一个上界\(u_0\)，偏序小于所有其他\(A\)的上界，则称为\(A\)的最小上界。
- 若\(S\)的子集\(A\)存在一个下界\(l_0\)，偏序大于所有其他\(A\)的下界，则称为\(A\)的最大上界。
偏序格定义（格的集合定义）：如果一个偏序集的每对元素（构成的子集）都有最小上界和最大下界，就称这个偏序集为格。
代数格定义（格的代数定义）：在集合 \(L\) 中定义两个代数运算 \(∨\) 和 \(∧\)，这两个代数运算满足：幂等律、交换律、结合律、吸收率，则称该代数系统为格。

温习离散数学相关知识，我们知道一个子集\(A\)可能有上界但无最小上界，有下界但无最大下界，“有界”是“有最界”的必要而非充分条件。

格，则是偏序集加上了对“最界”存在的限制，由于单元素集合上下最界就是其集合所含的唯一元素，显然成立，那么要求每对元素都有最界，那么任意子集就是有最界的（易证，略），从格的代数定义理解，实际上就是满足了交和并代数运算的完备性。

幂格

回到课堂上那个问题，集合的幂集与其上的包含关系构成格吗？

答案是肯定的。

我在机械工业出版社《离散数学及其应用》（Knneth H.Rosen 著）上找到了例题说明，而且，证明幂格存在也是简单的。

证明正如图所给，我写完整一些，\(S\)为集合，\(P(S)\)（有些习惯写为\(2^{S}\)）为\(S\)的幂集，证明过程如下：

首先证明\((P(S), \subseteq)\)是偏序集：

自反性，对于任意\(A \subseteq S\)（也即\(A \in P(S)\)），\(A \subseteq A\)，满足自反性。
反对称性：由\(A \subseteq B\)，\(B \subseteq A\)可推出\(A = B\)，满足反对称性。
传递性：\(A \subseteq B\)，\(B \subseteq C\)可推出\(A \subseteq C\)，满足传递性

所以\((P(S), \subseteq)\)是偏序集。

接着再构造性证明\((P(S), \subseteq)\)是格，从序理论证明有点困难（我确实没想到证交、并为最小上界和最大下界的方法），所以应用格的两个定义的等价性，我们尝试证明\((P(S),\cup,\cap)\)为代数格。

\(A,B \in P(S)\)，即 \(A,B\) 为原集合\(S\)的任意两个子集，则必为幂集的两个元素，构造\(C = A \cup B, D = A \cap B\)，显然\(C,D \in P(S)\)。

交换律：\(A \cap B = B \cap A\)，\(A \cup B = B \cup A\)
结合律：\(A \cap (B \cap C) = (A \cap B) \cap C\)，\(A \cup (B \cup C) = (A \cup B) \cup C\)
吸收律：\(A \cup (A \cap B) = A\)，\(A \cap (A \cup B) = A\)
幂等律：\(A \cap A = A\)，\(A \cup A = A\)

所以\((P(S), \subseteq)\)（代数表示为\((P(S),\cup,\cap)\)）是格。

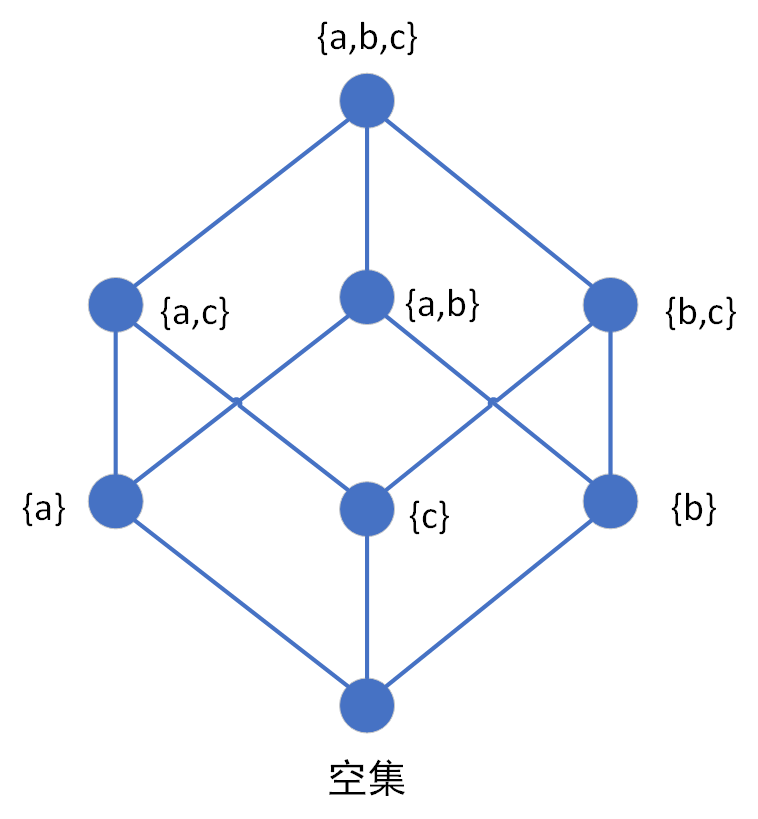
举一个简单的幂格的例子，并用哈斯图形式表示出来，即《离散数学及其应用》430 页所给的\((P({a,b,c}), \subseteq)\)的哈斯图。

显然，由图我们也可以直观看出，三元素集合的幂集是一个格，它有底和顶。

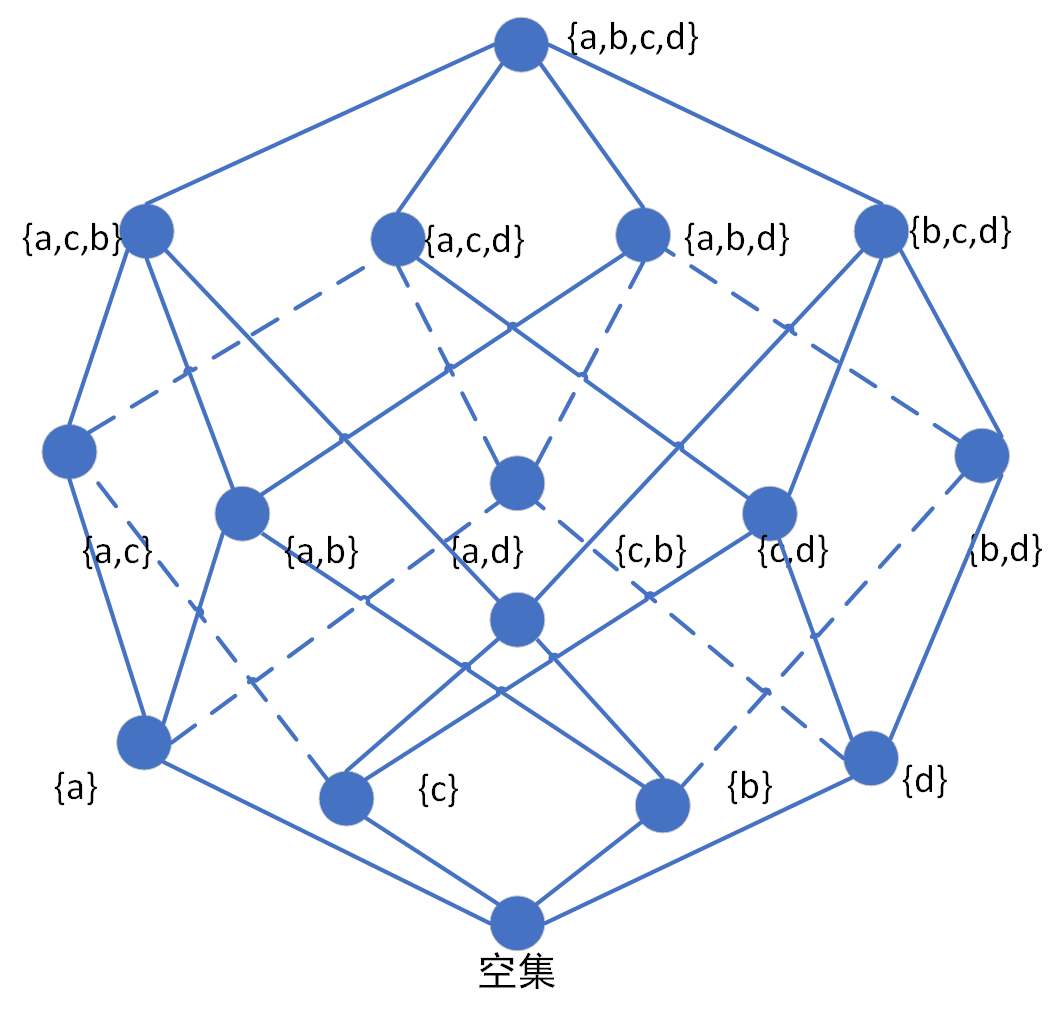
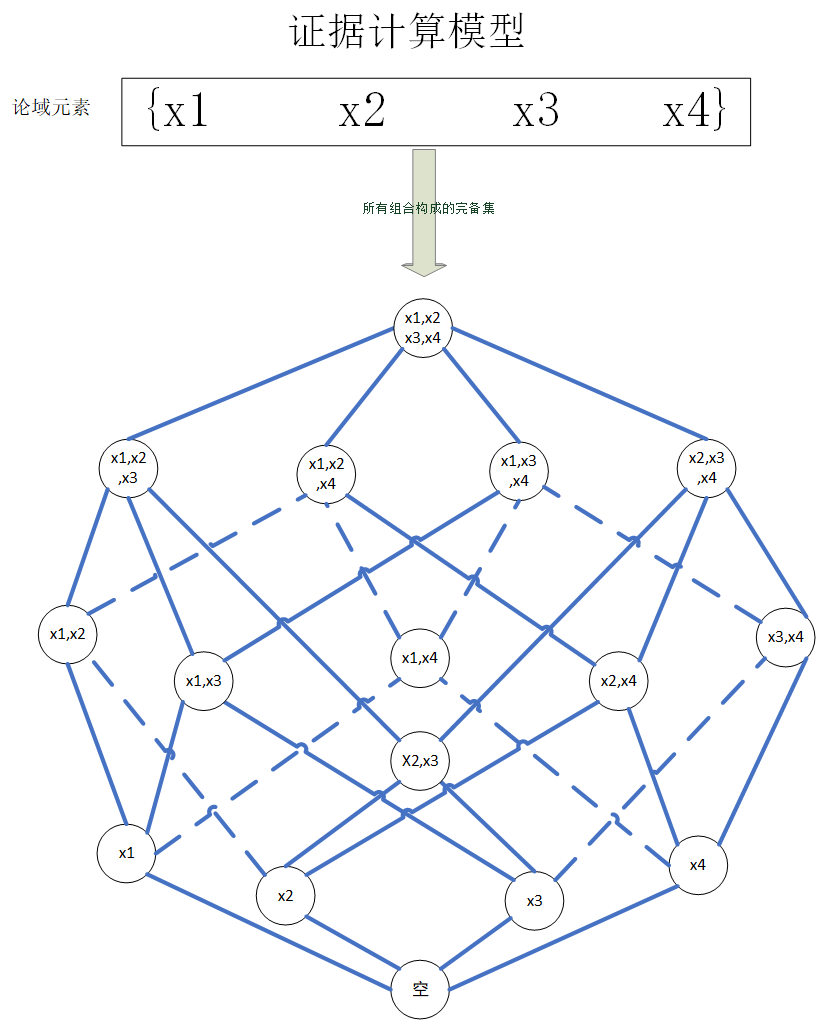
那么我自己绘制了一个四元素集合幂集的格图，如下

两种粒度

我自己的理解，粗糙集理论的粒度模型是不可分辨关系（等价关系）确定的划分构成的，而证据计算的粒度模型是对于有限集幂集构成的证据空间讨论的，由于\(2^{U}\)包含了所有的粒度（从空到完整）。

简单的数学表述：

问题\(X\)的所有可能取值构成非空有限集\(U = \{ x_1,x_2, \cdots ,x_{n-1}, x_n \}\)。

粗糙集模型：

（这里按照《基于粗集理论的多属性决策分析》（后文简称《粗集理论》）一书的习惯性表述来写）

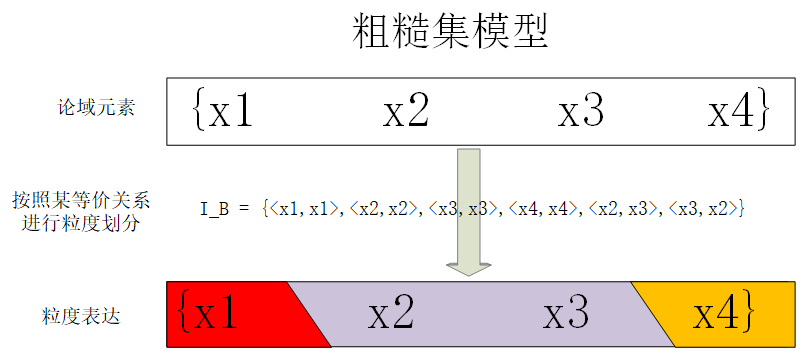
粗糙集一般应用在决策表中，引入全属性集\(A\)，则\(B\)属性集族定义一个不可分辨关系\(I_B = \{ (x,y) \in U \times U : f(x,a) = f(y,a), \forall a \in B \}\)，这个定义是针对决策表属性讲的（直观表述即两论域元素\(x,y\)对\(B\)属性集中任意属性列取值均相同，所以不可分辨）。

讨论空间：集合上的所有划分形成的空间

原子集（信息基本粒子）：等价类\(I_B(X)\)

复合集：原子集的任意并集
证据计算模型

讨论空间：集合的幂集空间

原子集/复合集（信息的各种粒度）：所有可能子集，其中单点集对应确定命题，复合集对应不确定命题

所以实际上证据计算模型我的理解是是给了从最细粒度（单点集）到最粗粒度（原命题）所有的粒度，并给不同粒度独立进行赋值。

粗糙集中近似与证据理论信度函数的关系

我们先来看定义

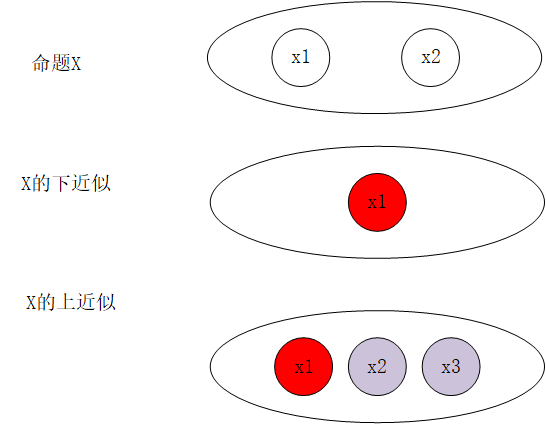
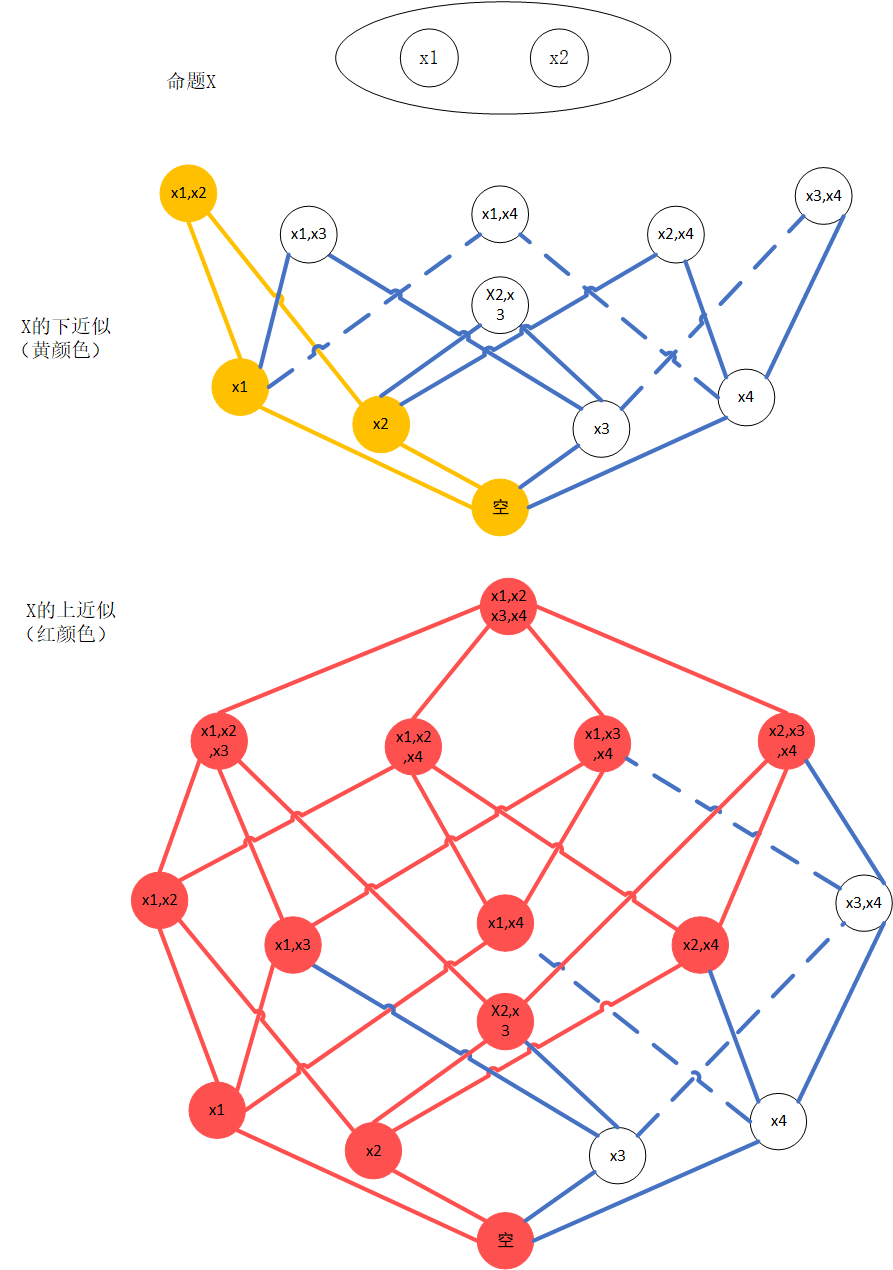
粗糙集的近似：

课件中：
- 下近似： \(\underline{apr}(X) = \{ x | [x]_R \subseteq X \}\)
- 上近似：\(\overline{apr}(X) = \{ x| [x]_R \cap X \not ={\emptyset} \}\)
《粗集理论》中：

设\(S\)为信息表，\(X\)为\(U\)的非空子集，\(B \subseteq A\)且\(B \not ={\emptyset}\)，集合\(X\)的\(B\)下近似和\(B\)上近似为：
- 下近似：\(\underline{B}(X) = \{x \in U : I_B(x) \subseteq X\}\)
- 上近似：\(\overline{B}(X) = \{x \in U : I_B(x) \cap X \not ={\emptyset}\}\)
实际上老师课件中给出的\(R\)实际上就是属性族\(B\)所定义的不可分辨关系（等价关系\(I_B\)），所以两种表述实际上只是形式不同而已。

我们不难发现，近似的结果仍为\(U\)的一个子集，近似运算实际上是定义在\(U \times U\)的
证据理论的信度函数

那我们再来看信度函数(信任函数和似然函数)，按照老师的课件上来，为了和上面对应把\(X\)，\(A\)表示调换了一下，没有实际影响。
- 信任函数：\(BEL(X) = \sum_{A \subseteq X} m(A)\)
- 似然函数：\(PL(X) = \sum_{A \cap X \not ={\emptyset}} m(A)\)
实际上我们已经发现其形式和粗糙集的“近似”有了相关性，为了方便进一步思考，我们将信度函数的计算拆分成两步——1. 找集合 2.概率累加。首先寻找满足条件的子集\(A\)，然后将其基本概率分配（bpa）\(m_S\)累加起来。

联系与区别

联系

X 均表示当前命题
下近似/信任函数表示命题完全包含的知识粒度（或其对应的取值）
上近似/似然函数表示与命题相交的所有知识粒度（或其对应的取值）

区别

粒度表示不同
- 粗糙集粒度是等价关系决定的等价类，划分的等价类两两不相交，而一个属性子集就确定了一个等价关系。
- 证据计算的粒度是所有可能子集，子集间还有包含、相交等关系，不需要由属性确定等价关系，所有子集的空间（幂格）本身就是完备的。
格对应的层级不同

虽然“格”的概念在粗糙集和证据理论中都有出现，但是其表征的含义，和所在的层级确是不同的。
- 粗糙集中，“格”出现在决策表约简过程中，不同属性集对应不同的等价关系\(I_B\)从而决定了细分偏序格中的位置，而不同的划分实际上表示了不同的“知识粒度”的不同。
- 证据计算中，“格”出现在粒度本身的定义中，由于该框架下知识粒度本身就有粗细结构（虽然基本概率独立赋值），其知识本身就呈现“格”结构。